ABC 326, AHC 025, Thunder 本 / IO, ST, State

競技プログラミング

訓練

先週の ABC 325 E を upsolve した。 Dijkstra の典型だったが TLE した。人の提出を真似て枝刈りをすると AC になった。

色々なダイクストラ高速化 (yosupo 氏) を見ると、枝刈りによって『何十倍も速くなる問題も』あるという (P15) 。オーダーは変わらないと思っていたが……？？

青 diff DP を 3 問解いた。 TEE を見ると約 2 ヶ月の周期性があったので脱したい。

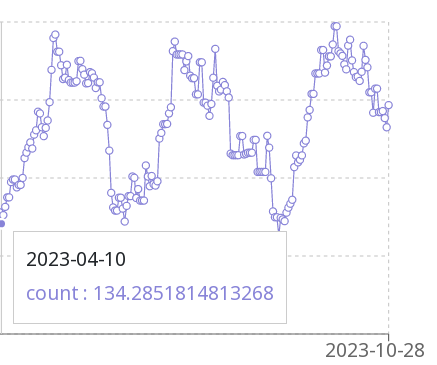
AHC 025

AHC 025 が終了した。複数の重りをグループ分けし、重さを平均化せよというインタラクティブ問題だった。

結果は緑パフォだった。個々の要素をソートして、当てずっぽうに組み合わせることしかできなかった。そろそろ対策してみたい。

ABC 326

ABC 326 に参加した。

A 問題ではセットアップが壊れていて焦った。

B 問題は算数だった。

C 問題では尺取り法 (two pointers) のテンプレートを使った。条件を満たす (l, r) 区間の一覧が返るようになっている:

twoPointers :: Int -> ((Int, Int) -> Bool) -> [(Int, Int)]
twoPointers len p = _ {-# 実装は汚いので省略…… #-}

添字バグに戸惑った。閉区間 [l, r] では len = r + 1 - l となるのが厄介だった。

尺取り法は 2 分探索で代替できない場合がある。たとえば第 8 回 PAST - L は 2 分探索だと TLE になった。

D 問題は枝刈りができず見送った。実装も大変だったらしい。まだ upsolve していない。

E 問題は期待値 DP として解いた。図のような遷移において、 \(E_i = \sum_j (E_j + \Delta x_{i, j}) p_{i, j}\) が成り立つ。実際、期待値の定義 \(E[X] = \sum_i x_i p_i\) に立ち返ると計算式を証明できる (省略) 。

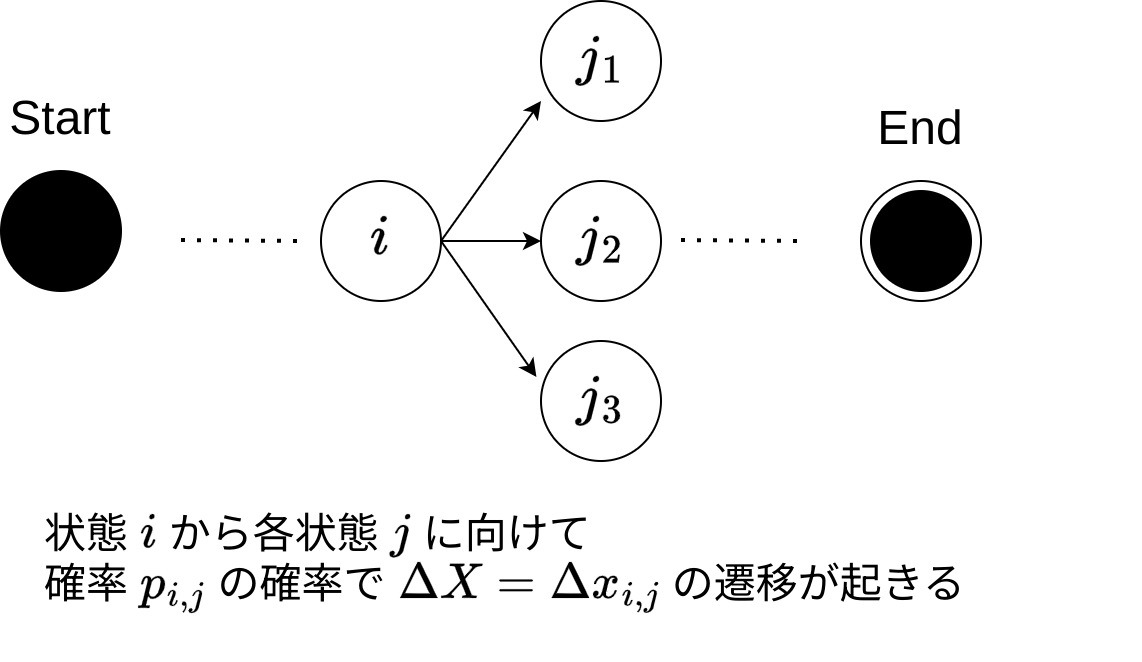
\(dp[i] := E_i\) はトポロジカル順に求める (終点から順に求める) 。今回の問題における遷移を整理すると \(E_i = \sum_j (E_j + \Delta x_{i, j}) \frac 1 N = (\sum_j E_j + \sum_j \Delta x_{i j}) \frac 1 N\) であり、それぞれの \(\sum\) をセグメント木と累積和から計算できた。セグメント木も累積和にした方が賢い。

確率変数 \(X\) などは雰囲気で書いており、人には伝わらないかも……。

F 問題は x, y 成分に分けると半分全列挙になるが、経路復元が間に合わなかった。 upsolve したい。

以上、 C 問題 (尺取り法) と E 問題 (期待値 DP) を貯金で乗り切った。

備忘録 (期待値 DP)

EDPC - J Sushi に通じる類題を考える。

1/2 の確率で表が出るコインがある。 3 回表を出すまでにコインを投げる回数の期待値は？

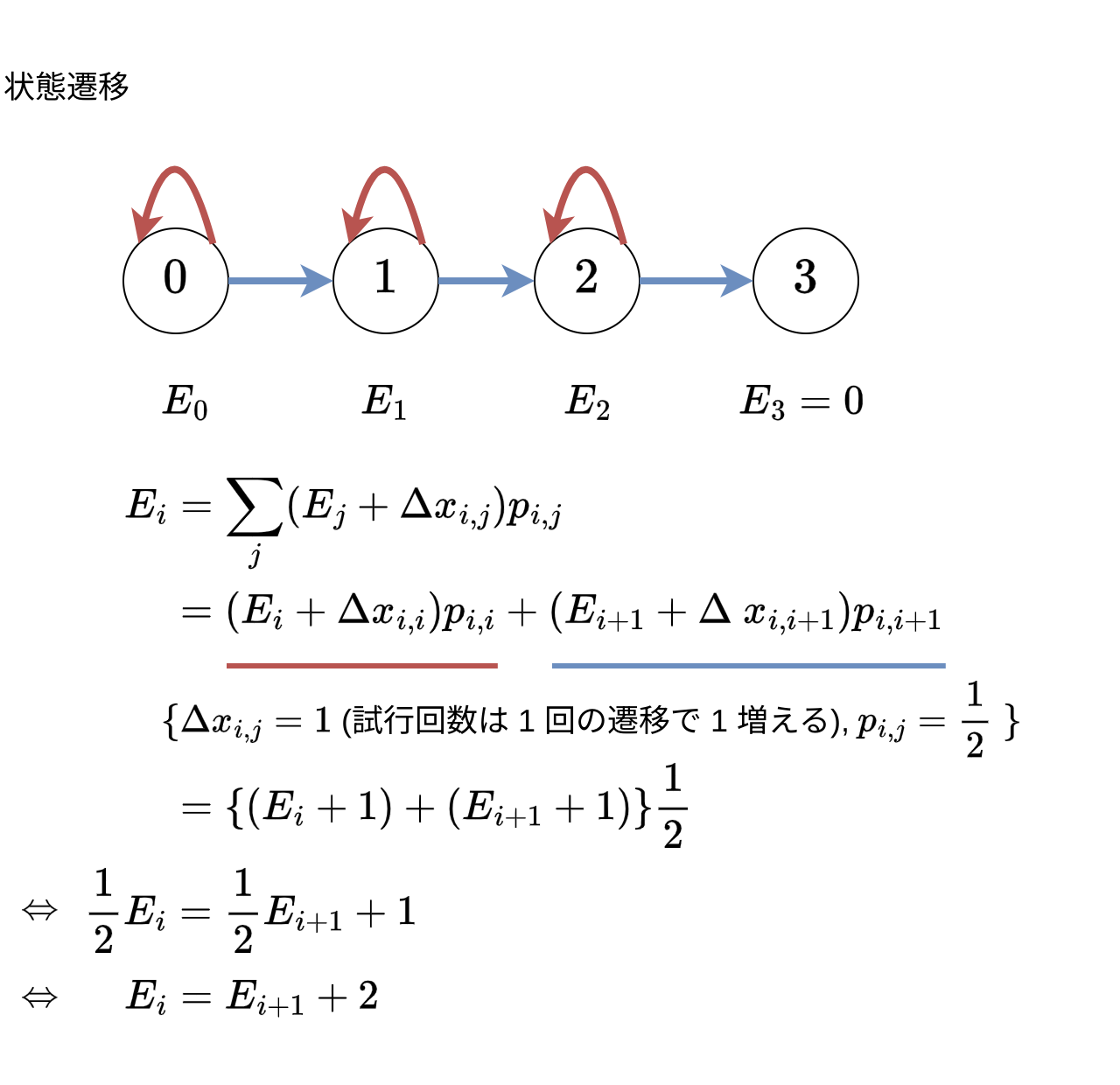
DP 的な式整理無しで解くのは無理な気がする。まず \(E_2 = \sum\limits_i p_i x_i = \sum_\limits{n=1}^{\infty} \frac n {2^n} = 2\) 。 \(E_1\) は……考えたくない。。

読書

Thunder 本

AHC 025 の結果に刺激を受けて、ゲームで学ぶ探索アルゴリズム実践入門を読み始めた。

著者: Thunder 氏

Haskell で取り組むため、 random パッケージを見た。 StdGen が乱数のシード (?) で、あるシード値からは常に同じ乱数が生成される (決定的である) 点が AHC 向けだと思った。

Software Design

Software Design 2023年11月号の Bram 氏 (Vim の作者) の追悼記事を読んだ。人生か……

Haskell

Qiita Conference 2023 Autmun Day2

naoya さんを (オンラインで) 見た！！！！

ツイートしなかったもの

『メンタルモデル』と音で聞いたのは初めてです

『ノイマン型コンピュータ』などの正確な描写が 🧠 に fit boxing

React, Elm, オニオンアーキテクチャなど現在と過去・似たものを結びつける考えがスマート

IO を計算機への命令と表現した端的な解釈で脳みそが脱皮

accumArrayDP って前から半環でしたっけ

shakutori が分からない

僕は『代数的構造』とか『計算』といった抽象的なものが見えたことが無くて『半環』とか accumArray のような具体的なものばかり考えています

いつもながら抽象的なものを手探りしている感じが面白かったです

`State` モナド

naoya さんと言えば、普段の投稿がぶっちぎっていて面白い。キーボード箱買い……棚買い事件はもちろん、 Haskell でも突き抜けている。最近は State モナドの使い方が腑に落ちて面白かった。

一方、そこに State モナドを使って再帰の過程でグローバルな領域に計算結果を書き込むようにする。すると途端に再帰の記述の認知負荷が下がって、楽になる。 pic.twitter.com/y0n64UKXpS
— naoya (@naoya_ito) October 7, 2023

この『いいね』数、みんな付いて来れなかったか……！

State モナドを immutable データに対する ST モナドのように扱えることが示されていて驚いた。むしろ、 ST や IO が State と似ていると考えた方が Haskell 的なのかもしれない。

`IO` の正体

mod_poppo 氏 unsafePerformIOではじめる愉快なHaskellプログラミングの結論によると、 GHC.IO は以下の newtype であるという:

newtype IO a = IO (State# RealWorld -> (# State# RealWorld, a #))

ほぼ State モナド (?) 。なるほど『純粋』関数型言語 Haskell だ。

しかしまだ IO と State が同じだとは思えない。以下でギャップを埋めてみた。

`runIO` は無いのか

State の evalState に対して、 IO の runIO は無いのか。これは main:: IO () に対して mainImpl = runIO main RealWorld が隠されていると解釈すれば、 main も通常の Haskell であると言える気がする。たぶん。

可変変数に関して

State ではすべての状態が文脈の中に隠れているのに対して、 IO では ref <- newIORef (0 :: Int) のように識別子が露出する。この違いをどう捉えるべきか。

まず ref は IO が使用するハンドル？参照？であって、可変変数ではない。 ref 定数である。そして ref ではなく readIORef や writeIORef のような外界 (RealWorld) に触れる操作の方が特別 (mutable) であると考えられる。

-- `IORef` のサンプルコード:
ref <- newIORef (1 :: Int)
x1 <- readIORef ref -- `ref` が参照する値をコピーして読み出す (`1`)
writeIORef ref (x1 + 1) -- 参照先の値を更新
x2 <- readIORef ref -- `ref` が参照する値をコピーして読み出す (`2`)

また State モナドの中にアロケータ相当のデータ (たとえば IntMap Int) を入れれば、 State の文脈で以下のようなコードを書くことも不可能ではない:

ref <- newIntRef (0 :: Int)
x1 <- readIntRef ref
writeIntRef ref (x1 + 1)

よって IO はアロケータ (など) が入った State モナドであるとみなせば、 State と見かけ上の差が無いと言えるはず。

Mutable な primitive 操作

State と IO がほぼ同じものであることは分かった。真の違いは、 writeIORef など IO でのみ許される関数の実装にある。ここでメモリ領域の書き換えを行い、 RealWorld -> RealWorld という幻想を作っているはずだ。

まず writeIORef は writeSTRef を使って実装されていた。 writeSTRef は次の通り writeMutVar# に依存している:

writeSTRef :: STRef s a -> a -> ST s ()
writeSTRef (STRef var#) val = ST $ \s1# ->
    case writeMutVar# var# val s1#      of { s2# ->
    (# s2#, () #) }

そして writeMutVar# の関数定義は base パッケージに無かった。 How are mutable arrays implemented in Haskell? を見ると、 writeMutVar# を始めとした primitive な操作は prim-ops に定義されているらしい。その実装は Haskell ではない。

Haskellのキャラクター作った pic.twitter.com/fu1jX2yKMP
— Hideyuki Tanaka (@tanakh) May 21, 2014