競技プログラミング

オフ

今週は Haskell 本にかかりきりだった。読書も無し。

今回の ABC では、小さな関数を積極的に作ろうと決めた。

ABC 327

ABC 327 に参加した。 5 完 (A~E) だった。

A 問題 では長さ 2 の窓を左から右へ流し、 or $ BS.zipWith p s (BS.tail s) の形で解いた。

B 問題 では平方数と勘違いして 2 分探索を始めた。困ります。。 \(1^1 .. 17^{17}\) 程度までが解の候補であると気づいて全探索した。俺の埋め込みが火を吹く……ほどでもない。

C 問題 はゴリゴリ解いた。 2 次元配列を列ごとに走査する関数を作っても良い気がした。

D 問題 では長さが奇数のループができたら No であると判定する方法を考え、実際に 0, 1 を塗ってみれば良いと気づいた。タイムラインでは 2 部グラフ判定と言う人が多かった。確かに！

全点から DFS/BFS するのは競プロ的な富豪スタイルだと思う。全探索という概念を知って驚くのと似ている。この辺の計算量の感覚が身につくと茶色コーダーになれるんだろう。

ところで BFS を空で書けと言われると厳しい。 concatMapM か、キューを使うか……。やはり Haskell では再帰 DFS が 2 部グラフ判定の最も簡単な実装となる。

E 問題 は読解が大変だった。ナップサック問題じゃん (´･_･`)

F 問題 は PAST でありがちな平面走査の問題だった。解けない。

QuickCheck で E の誤答を検証する

E 問題では DP テーブルを三角形にしたため AC できた。正方形のテーブル全体を使用した場合は、本来無効なセルに何度も \(0.9\) がかけられて行き、最終的に牙を剥くらしい。

\(0.9^N\) が発生するにせよ、 max による緩和で消える気がして納得できない:

ghci> (!! 5000) $ iterate (* 0.9) (-(10.0^18))
-1.6313501853428285e-211
ghci> max 1 $ (!! 5000) $ iterate (* 0.9) (-(10.0^18))
1.0

そこで WA となるテストケースを見つけるために、 QuickCheck を使ってみることにした。

公式サイトが無い。 README もほぼ空。 Haskell のコミュニティは謎だ。

人のブログを読んで、乱数の Gen を forAll に食わせてテストケースを作ることができると理解した:

import Test.QuickCheck qualified as QC

prop :: QC.Property
prop =
  -- 1 <= N <= maxN
  QC.forAll (QC.choose (1, maxN)) $ \n ->
    -- [x | 1 <= x <= 5,000]
    QC.forAll (QC.vectorOf n (QC.choose (1, 5000))) \xs ->
      let !xs' = U.fromList xs
       in solveAC n xs' QC.=== solveWA n xs'
  where
    maxN = 1000

runTest :: IO ()
runTest = QC.quickCheck prop

-- 実行制限時間 [ms] を設けるなら、次のように書けば良さそう:
-- QU.quickCheck $ QC.within (1000 * 1000) prop

REPL から QuickCheck を実施してみた:

$ stack repl e/Main.hs
ghci> runTest

遅い。 HeavyCheck という感じだ。やはり REPL からの実行ではコンパイル実行にならないことが分かったので、一旦 main 関数から runTest を呼ぶようにしてみた:

main = runTest

$ cabal run e-exe
<巨大な出力>

高速で実行できたが、テストケースがデカ過ぎて一望できない。 maxN = 1000 で再度実施した:

$ cabal run e-exe

 *** Failed! Falsified (after 6 tests):
835
[2315,1697,2340,2332,4072,3338,3072,1816,380,1763,2422,4562,3200,4568,4553,4049,825,4335,2931,2017,668,3548,1300,415,4785,1941,790,18,2053,3246,2959,830,3981,4993,4504,2431,3031,1964,3273,611,2289,4163,481,2085,4642,2762,2399,2194,1584,4961,2294,130,4790,4297,3007,4318,2210,1812,2393,404,231,3151,2973,1260,756,340,2208,4719,4717,2348,3735,440,4516,3979,84,2467,2570,1699,3933,46,2664,1274,2412,2659,2205,4102,1089,4797,1593,1147,1514,3406,3139,3121,2068,412,4327,2475,755,2294,333,1198,1811,1330,1153,545,3837,2338,4841,2152,2534,4390,1926,4782,1538,556,1318,1507,1975,3481,1084,3705,2025,1934,661,3448,638,369,925,3096,1295,4802,2359,3963,2740,1550,104,3202,4706,272,1358,1008,3518,4808,3905,1424,65,1581,4261,700,4440,2511,4893,3060,2100,1988,2425,389,1225,1842,3667,2525,2320,838,449,1965,4289,3939,2575,2499,1277,1564,1433,4260,4666,78,1068,3061,1314,1943,2591,4867,2349,817,1720,4253,2209,2905,444,887,3323,3958,3163,4208,1659,328,536,75,4162,2875,1440,4046,4839,732,4912,4138,3728,2349,3944,4810,4353,1464,4700,3491,2078,3924,1064,742,4996,4427,1292,2521,3551,4076,3843,2189,1064,2172,2518,706,1627,4877,3651,1035,3287,2351,3359,1053,1063,2907,4808,2793,1614,3449,4821,506,1231,2049,1861,1792,585,2879,2279,3159,2665,3799,4975,242,1865,3570,3893,4092,1633,220,2502,3262,378,3565,4699,478,3724,1011,108,4049,1243,404,2,3123,4305,4195,4141,3378,272,1989,285,480,3718,1460,2766,4195,2535,3325,3780,918,3772,50,1411,2935,2906,4352,3782,1632,746,2574,3861,2991,1259,1620,3635,3756,3472,1510,2214,2744,994,2100,1008,1115,3661,1040,3233,4274,2640,4595,4538,2328,4138,3948,1711,1057,3542,2001,173,3267,4096,4665,1647,2879,1168,1314,728,1549,4111,4526,3040,24,272,4941,4345,4169,1019,775,2056,3134,918,3090,2142,1527,936,2779,2184,2975,1810,1386,3054,4013,3252,4184,1516,4859,950,2906,2983,181,1758,1292,2549,3651,3637,3057,2384,3039,4757,4243,1903,249,3338,461,2797,3185,3303,3682,4930,4247,3882,667,817,2253,2023,2228,933,891,2433,477,3525,4548,1196,3959,803,4109,599,1750,2315,3531,2097,1490,4999,898,4570,4547,96,401,1841,1592,2255,4557,575,2693,2838,1960,199,3066,1811,4792,3839,1309,3079,675,1105,2976,2524,542,3306,1893,4422,3760,1387,4783,2236,4659,1702,4339,1944,113,583,1872,1427,3474,4166,3749,3417,2572,4874,2282,4911,4840,154,2396,4789,4001,1060,1669,1654,4814,2433,4399,1335,3545,3318,2287,1998,3704,4519,749,4276,514,4884,3698,4726,1839,4752,4930,3696,1267,3503,4957,2970,2596,1697,1101,2668,221,1251,1702,2605,3058,1742,3173,3895,1724,247,2331,2617,3918,3243,1714,4512,3919,1596,3405,877,1118,769,836,447,786,958,79,3078,1415,956,4116,116,1192,3780,1066,4036,4995,1457,4838,434,2226,839,2009,3285,123,4316,2974,352,4058,4104,4365,2661,1466,4898,451,2225,258,1947,2081,4554,4818,332,2523,2922,4944,1821,3423,2957,2678,3521,2649,2078,1218,4007,1547,3260,2040,2688,4297,4508,4714,4782,2886,230,507,4824,3446,2810,4033,280,752,123,4285,1869,1776,4854,3098,583,1453,4235,631,4258,938,3729,1188,1008,3461,3249,3432,987,4162,3177,3991,215,2930,4574,4459,3341,1952,4193,4308,2861,1947,3074,3388,428,2710,2038,3788,3059,227,3995,4654,4755,4961,611,4005,1144,2471,318,1366,422,3328,1995,3781,294,413,1411,414,3868,4725,3724,1838,4959,3070,4856,3369,4827,2097,2613,1205,363,2541,3934,4200,2592,4229,2645,2957,4383,3225,2063,161,1510,3020,384,4541,3471,2642,2649,4703,1357,2907,2954,4458,3173,82,1542,1248,234,1908,4420,3547,3924,2773,1300,3151,3757,4140,3359,4478,521,4971,4315,3088,4098,3440,733,4472,4699,1606,3136,3546,147,671,34,581,720,1088,1054,3605,4421,2347,2369,82,4403,2490,4137,4420,3749,4768,217,1234,1467,678,261,2143,3999,4476,1724,3706,3762,2740,2122,3816,4879,352,2040,1482,495,2774,1118,222,4877,271,2155,4128,687,1890,1485,4132,3111,3953,3272,76,811,2942,718,3870,706,4582,3425,1776,469,3897,3165,4119,2555,958,1903,2087,4403,4632,770,3148,854,3582,1692,2783,2555,3829,3423,4469,1653,852,2806,1241,2578,4593,4971,1867,1490,4656,1199,1968,3736,4931,2082,3727,4206,103,1887,4486,3006,2015,2164,3687,528,2566,2324,3444,2551,3140,3359,3798,4194,893,2835,3428,731,3670,4842,2234,2361]
4811.146865958838 /= 4829.74309692967

よっしゃ！　見つけたぞ！

それで、どうして間違ってるんですかね…… (´･_･`) ?　全然 shrinking してくれない。でも、もう満足しちゃったんだ。

読書

何も読んでいない。

ラムダノートの 実践プロパティベーステスト ― PropErとErlang/Elixirではじめよう が話題だ。 すごい Haskell も 実践TLA+ も流行ったけれど、実際に読んだのは何人くらいだろう。

短いなー人生。

Haskell 本

Haskell Advent Calendar 2023 の 23 日目の記事に予約した。購読者 13 人。衰退する運命にあるというか、そもそも流行っていないというか……。

進捗: 10%

標準入出力、 Cabal スクリプト、 ABS などに関してざっと書いた。クエリ処理とキューの不在など、序盤の難所に入れそう。

表紙

表紙のラフが来た！　良かった。ガイコツ案の未練はもう無い。

当初は巨大なスクラップのような book を予定していたが、できるだけ歩み寄った内容を目指したくなった。うーん無理かも。

環境構築

vector-algorithms の sort が遅い件

haskell-jp におけるコメント の通り VAI.sort が遅くなっていたのを体験できた。

ABC 269 D - Do use hexagon grid

State モナドで immutable データ構造を持ち回す

憧れの方法をやってみた。

deepseq

ABC275 A～E+F をHaskellで

foldl' 中の step 関数の中で force を実行すると速くなる場合がある (deepseq) 。実際 force を入れると、リストを使ってナップサック問題を解いた場合も十分な速度が出た。

sparseListForced :: Int -> U.Vector (Int, Int) -> Int
sparseListForced maxW = maximum . map snd . U.foldl' step s0
  where
    s0 = [(0, 0)] :: [(Int, Int)]
    step wvs (!dw, !dv) =
      force . merge wvs $ filter ((<= maxW) . fst) $ map (\(!w, !v) -> (w + dw, v + dv)) wvs

    merge :: [(Int, Int)] -> [(Int, Int)] -> [(Int, Int)]
    merge xs [] = xs
    merge [] xs = xs
    merge xxs@(!x : xs) yys@(!y : ys) = case compare (fst x) (fst y) of
      LT -> x : merge xs yys
      GT -> y : merge xxs ys
      EQ -> (fst x, max (snd x) (snd y)) : merge xs ys

ただしサンクが溜まっていない状態で force すると、余計なコストがかかるだけのようだ。

ベンチマーク

criterion や tasty-bench でベンチマークテストを実施できる。

コードとしては、テストケースを列挙するだけだった:

main :: IO ()
main = do
  ((!n, !w), !input) <- readInput
  defaultMain
    [ bgroup
        "knapsack"
        [ bench "dense-unboxed-vector" $ whnf (denseU w) input,
          bench "dense-boxed-vector" $ whnf (denseV w) input,
          -- 略
        ]
    ]

Cabal プロジェクトの設定としては vector が参考になった。 tasty-bench の方が軽くて良かったが、 criterion は結果の時間軸を対数にして表示できるのが良かった:

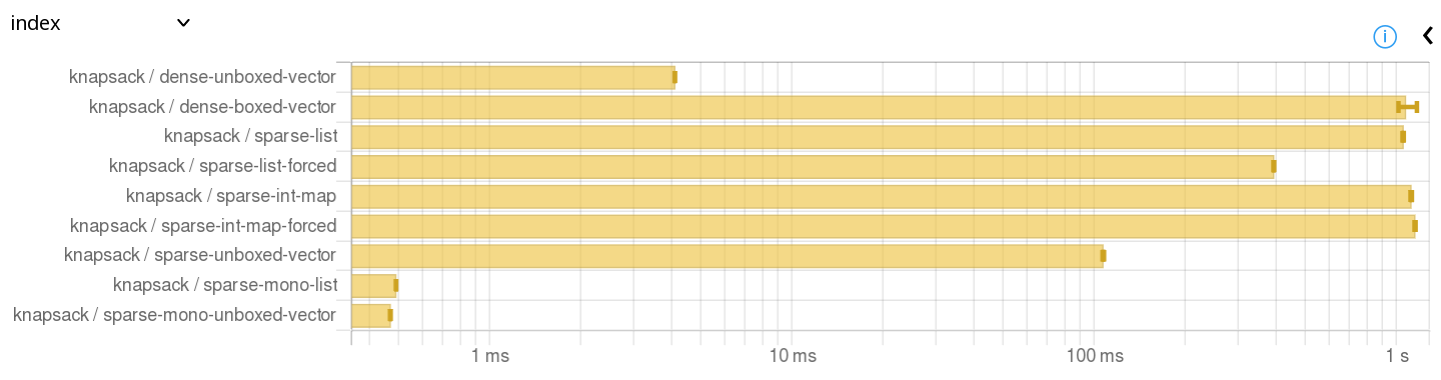
2023-11-05-criterion.png
Figure 1: EDPC D - Knapsack 1 のベンチマーク結果。

vector は tasty-bench を使用しているが、 criterion とほぼ共通の API のため乗り換えは簡単。

The Haskell Unfolder series

ざっと観たはずだが……

  1. Episode 1: unfoldr
    unfoldr の定義を見る。何を表現できて、何が表現できないか確認する。
  2. Episode 2: quantified constraints
    @ は at を表していて、 Proxy @Int は instantinate Proxy @t Int と読まれる、はず
  3. Episode 3: injectivity
    型族の話だった。 Functional dependency で単射にできる。だからどうなんだっけ……
  4. Episode 4: falsify
    falsify によるプロパティベーステスト。飛ばしてしまった。
  5. Episode 5: composing left folds
    readFile の返り値に対して 3 回イテレートすると、処理時間が定数倍ではなくなった。
    TODO: なぜ？
    3 回 readFile すれば定数時間になった。また foldl パッケージを使うと、複数の畳み込みを 1 回の実行で済ませるコードが簡単にかける。

その他