ABC 346 / SegTree, ContT

ABC 346

ABC 346 に参加しました。

A 問題

この問題から学べたことは、 f<$>id<*>h は f<*>h と書けることです。

main=interact$unwords.(zipWith((show.).(*))<*>tail).tail.map read.words

B 問題

w, b の数を数える替わりに、ソートして比較しました。

main :: IO ()
main = do
  (!w, !b) <- ints2
  let s = concat $ replicate 400 "wbwbwwbwbwbw"
  let pats = V.generate 200 $ \i -> sort . take (w + b) $ drop i s
  let res = V.any (== replicate b 'b' ++ replicate w 'w') pats
  printYn res

C 問題

補集合を考えて、 $1 .. K$ の総和から $\mathrm{sum} \{ A_i | A_i \le K\}_i$ を引いて解きます。

リストを使う場合は、 extra パッケージの nubSort を使って $\{ A_i | A_i \le K\}$ を作るのが良いと思います。 nub . sort よりちょっと速いです。

D 問題

DP として解きました。

E 問題

クエリを逆順に処理する発想が無く、重たい実装になってしまいました。色 0 の処理もゴリ押しです。水 diff は堅いと思っていました。

upsolve すると単なる畳み込み (+ 後処理) になりました。

F 問題

全然解ける気がしないですね……

正格セグメント木のボトムアップ実装

正格セグメント木を再実装しました。 $N=5000$ で $O(N^2 \log N)$ が通らなかった問題も、強引に AC できるようになりました。

以下では高速化に役立った『再帰実装』、より適切に言えばボトムアップ実装をメモします。

Haskell においては (ほぼ) すべてのループが再帰ですから、ボトムアップ実装と言わねば意味が通らないと思います。

最高の資料

やはりえびちゃん氏の資料が 1 番です。ローリングハッシュのモノイドも出てきました。

非再帰セグ木サイコー！一番すきなセグ木です

区間取得の 2 種類の実装

典型的なセグメント木は、 $[0, N)$ 区間に対する完全 2 分木です。高さ $h = \left \lceil \log_2 N \right \rceil$ で、葉の数 $N = 64$ の場合 $h = 6$ です。

セグメント木は $[l, r)$ 区間の畳み込みを $O(\log N)$, つまり高さ $h$ に比例する程度の時間で計算できます。この計算の実装は、トップダウンとボトムアップの 2 通りあります。

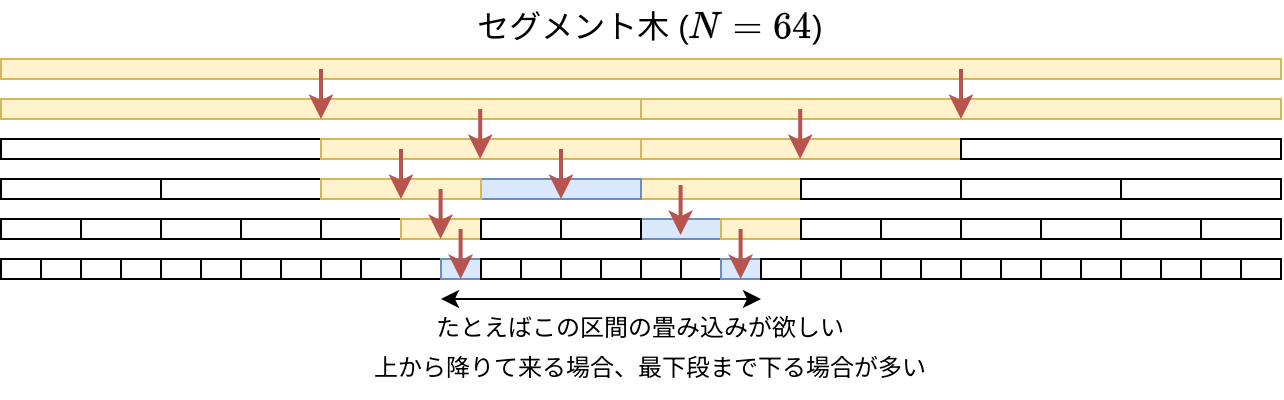
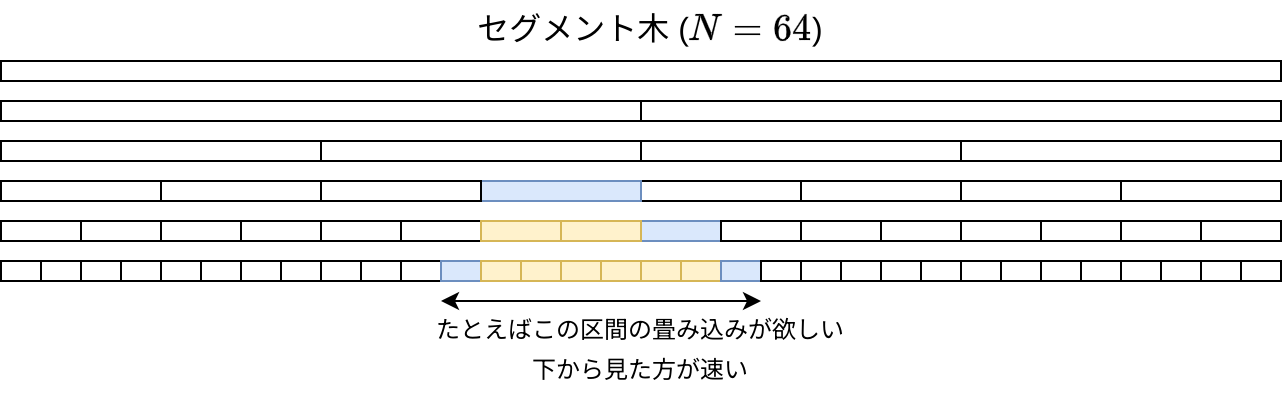
図に描いた通り、明らかにボトムアップ実装の方が速そうですね。

ボトムアップ実装が常に速いのか

ランダムな $[l, r]$ 区間が与えられた場合、トップダウン実装においては 3/4 の確率で最下段のデータを読む必要があります。そのため (厳密な期待値は分からないですが) ボトムアップ実装の方が高速……っぽいです。

Segment Tree を少し速くするのベンチマークを見ると、ボトムアップ実装が倍程度速いようです。証明は……放っておきます。

ボトムアップ実装の詳細

PAST 上級本における遅延セグメント木の実装に準拠して実装しました。

1-based index

頂点の番号を 1-based index にした場合、親 or 子への移動をビット演算で表現できるため、若干高速になります。左シフト (.<<.) で左の子、左シフト後に最初のビットを建てる (.|. 1) ことで右の子、右シフト (.>>.) で親頂点に移動できます。

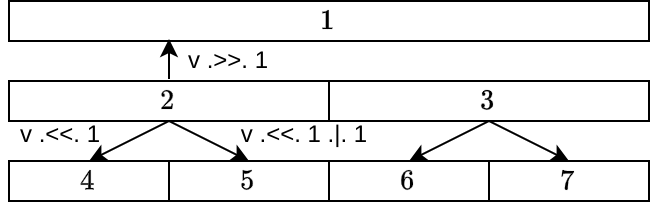
特に遅延セグメント木の実装の際は、 1 回の bit 演算で n 個上の親に移動できるのが便利です。

畳み込み

畳み込みの計算は、左右から (壁抜け + 天井破り) を繰り返して実施します。セグ木を移動するマリオが見えます。

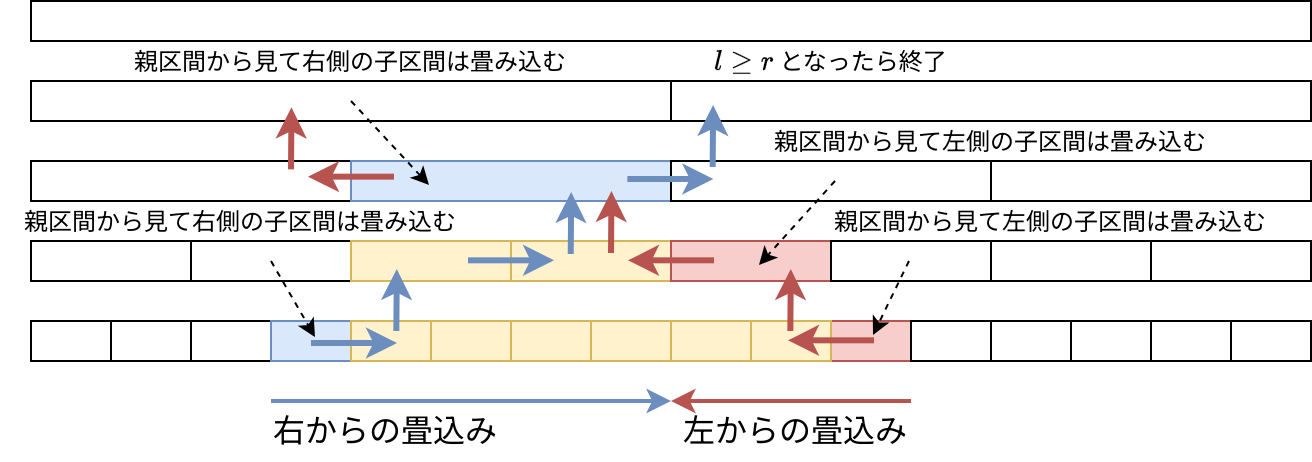
僕の中ではこの処理を glitching fold と呼んでいます。慣れればこっちの方が実装も簡単らしいです。

API

Monoid a を制約にしました。今やモノイドを前提としたほうが簡単に見えます。ただし Max Double, Min Double は成り立たないため、咄嗟にモノイドを自作する必要があるかもしれません。

関数は cojna/iota の Data.SegTree.Primal を参考に生やしました。 ac-library も似た関数を持っているようです。

方法	命名	他の命名候補	備考
1 点取得	`read`	`get`	便利です
1 点更新	`write`	`set`, `insert`	既存の頂点なので `insert` というよりも `write` でした
区間取得	`fold`	`prod`, `query`, `append`, `rangeGet`	`unsafeFold` かも
区間取得 (`Maybe` 型)	`foldMay`	`safeFold`	safe パッケージに倣います
全区間取得	`foldAll`	`foldWhole`, `readAll`	便利です
2 分探索	`bsearch`	`lowerBound`, `upperBound`

Misc

精進談義

交互 (interleaved) な演習の方が学習効率が高い説
naoya さんの ABC345 振り返りが面白かったです。自分の成長は主観では正しく測れないことを覚えておきたいです。
茶色コーダーになるのが難しい件について
1 色上を目指すのは常に困難が伴います。僕自身、半年かけて何とかレーティングを維持するだけの状況です。クソ……うんち難しいです

競プロ見聞録

ADT

AtCoder Daily Training (ADT) で 4 連敗しました。半年前の自分が 50 分で通した問題に 100 分かかり、地頭が既にピークよりも下にあるという困惑と納得がありました。

$\log N$ のサイズ感

ABC 227 C - ABC conjecture がどうしても解けませんでした。原因は、 2 分探索すると $\log_2 N$ が大き過ぎて TLE したことでした。

$\log_2 10^9$ が 30 程度です。 2 分探索無しでも 300 ms 程度の解答だったので、 10 倍以上の低速化がかかるとすれば通らないわけですね。こういう知識と経験で立ち回ります。

集合の分割

グループ分けの問題は、集合 DP や DFS によって解ける場合があります (ABC 310 D - Peaceful Teams, 典型 045 - Simple Grouping など) 。この DFS は集合の分割 (partition) の列挙なんだって ChatGPT が言っていました。

群論への第一歩にも分割が出て来ます。競プロをやると基礎教養への感度が上がりますね。 TRPG をやると頭が良くなるってひよりんニキも言っていました。

`ContT` で大域脱出

ContT モナドが (僕の) 注目を集めています:

継続とは何かを棚に上げ、試しに使用してみます。たとえば $2^n \ge x_0$ を満たす $2^n$ を求める関数があります:

-- >>> calc1 14
-- 16
calc1 :: Int -> Int
calc1 x0 = until (>= x0) (* 2) (1 :: Int)

これを Rust で手続き的に実装すればこんな形で:

fn calc_2(x0: usize) -> usize {
    let mut x = x0;
    while x < x0 {
        x *= 2;
    }
    x
}

Cont を使って手続き的な実装にすれば以下の通り:

calc2 :: Int -> Int
calc2 x0 = evalCont $ callCC $ \exit ->
  flip fix (1 :: Int) $ \loop acc -> do
    when (acc >= x0) $
      exit acc
    loop (acc * 2)

無駄に ContT を使えばこうなります:

calc2' :: Int -> Int
calc2' x0 = (`execState` (1 :: Int)) $ evalContT $ callCC $ \exit -> do
  fix $ \loop -> do
    acc <- get
    when (acc >= x0) $
      exit ()
    put (2 * acc)
    loop

ST や IO などの文脈の元でも ContT が使用できます。 for_ .. を大量にネストする場合などは、 Cont / ContT を使うと実装が簡単になります。パフォーマンスと利便性を両立するためには、もう少し深い理解が必要かもしれません (なぜか遅かったので……) 。

なお PrimMonad m => PrimMonad (ContT r m) が提供されているため、たとえば ContT ()(ST s) は PrimMonad を実装します。 lift する必要はありません。

キーボード

Ben Vallack はレイヤ切り替えのみで 16 キー操作を実現しましたが、 taipo レイアウトにおいてはキーの同時押しを使用します。常に両手で交互にタイピングできるのが強みのようです。やってみたい。

こちらの方も同時押しを嗜まれるようです。

参考にならないでしょうが、私の自作キーボードにおけるキー数の減らし方。その考え方の1例を雑な画像にしてみた。
指を伸ばして押下するよりも、Home Row絡みの複数キー同時打鍵の方がずっと楽だわ……という発見に基づき、Combo(ZMK)を多用しています。

Different strokes for different folks♪ pic.twitter.com/Ki23JTacrt
— がらくたでぶ (@garakuta_dev) January 25, 2024

この方の操作方法は不明ですが、やはり変態なのは間違いないでしょう。

[xiao ble] [pmw3610 トラックボール] [16キー V字] [lofreeスイッチ] [17mm 狭ピッチ]

第一段階クリア〜

あとは、Bluetooth入力・バッテリー運用・ケース作成ですな〜#自作キーボード pic.twitter.com/1isuuh7HE7
— 非ガンダム (@kaiiiiiiiiiiiak) March 13, 2024

この手のキーボードを簡単に入手したいものですが……。