ABC 353 / Convolution (予習)

ABC 353

ABC 353 に参加しました。何とかレーティングをキープできました。

A 問題

y+0 のように +0 を入れると read が整数型に推論される技を知りました:

main=interact$show.f.map read.words;f(_:h:x)=head$[i|(i,y)<-zip[2..]x,y+0>h]++[-1]

B 問題

% 演算子を定義し、関数呼び出し時の空白の数を減らしましょう:

main=interact$show.(0%).tail.map read.words
a%[_]=min 1a
a%(k:y:r)|a+y>k=1+0%(k:y:r)|0<1=(a+y)%(k:r)

C 問題

\(A\) をソートします。 \(\bmod\) と言わず \(10^8\) を引くことにすれば、一括処理できます。

\(i\) を固定したとき、和が \(10^8\) を超え始める点を見つけるためには 2 分探索または尺取り法を使います。 Haskell で実装する尺取り法の必勝法……を考え始めることの検討を加速します。

D 問題

ゴリ押しするか簡単な解法を考え抜きます。

私はゴリ押ししました。日記もゴリ押しに一塩です。

E 問題

これは輪を通る弦の組み合わせの数をカウントする問題だと思いました。先頭の文字でグループ分けしつつ、 1 文字ずつ剥いて行けば解けます。

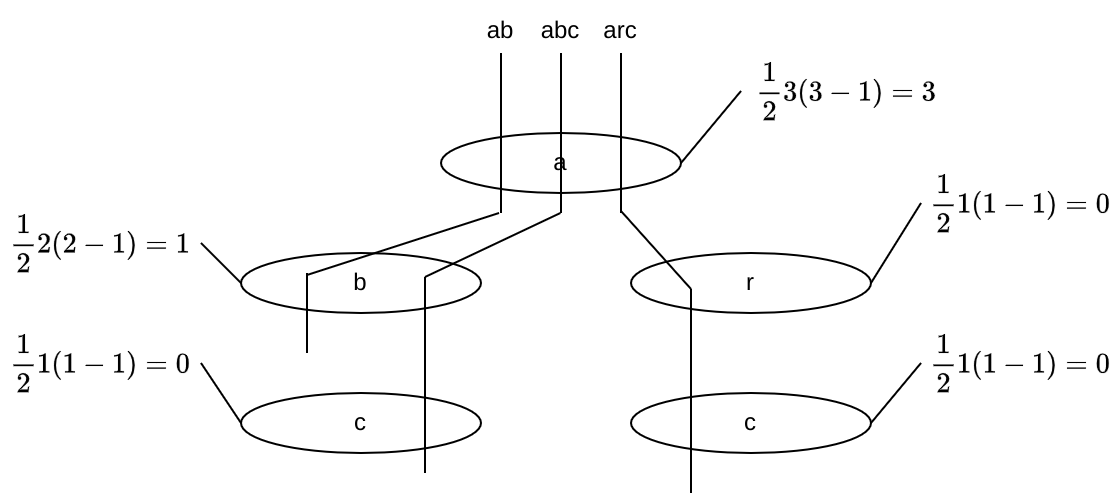
なお文字列ソートの計算量は \(O(N L_1 (\log N + \log L_1))\) 程度らしいです。今回は文字列長の総和 \(L \le 3 \cdot 10^5\) のため \(N = L_1 = \sqrt L\) とすれば \(O(L \log L)\) ？　速いですね〜 (読もう……)

G 問題

EDPC - Z と同じ問題に見えました。絶対値を外すため、 CHT に 2 本ずつ直線を追加していけば解けるはずです。 CHT は未習得の高度典型なので解けませんでした。

ところが絶対値を外して現れた式は、単なる 2 つの Max であってセグメント木 2 本に載ります。解けるべき問題でした。

なお CHT に似た何かがある？　みたいなので、 CHT に挑む時までに gksato さんの提出を読み込んでみようと思います。

G. ある市場(T, P)の以前に左で行われた市場の中で最善のもの、みたいなクエリが解けると良い。これは割と抽象化できるパターンだが言語化がむずい。
doEvent :: (Position, EventResult) -> (Position, EventContent) -> Maybe (Position, EventResult)
instance Ord Position (続)
— 符号/gksato (@Fine_sugar_hill) May 11, 2024

Convolution (予習)

高度典型: FFT/NTT/Convolution の勉強ノートです (未実装) 。

内容は誤りだらけです 。真剣に読まないでください。

三角基底による関数の展開

まずはフーリエ変換をエアプします。フーリエ解析―基礎と応用を参考にしました。

ボトムアップかつ天下り的に行きます。

冪級数展開 (Taylor 展開)

三角関数のように無限回微分できる関数は、冪級数の形に展開できることが知られています:

\begin{aligned} f(x) &= \sum \limits_{n=0}^{\infty} \frac {f^{(n)}(x_0)} {n!} (x - x_0)^{n} \bigg|_{x_0 = 0} \\ &= \sum \limits_{n=0}^{\infty} \frac {f^{(n)}(0)} {n!} x^{n} \end{aligned}

三角関数と指数関数を \(x_0 = 0\) の回りで冪級数展開すると、オイラーの公式 \(e^{ix} = \cos x + i \sin x\) が得られます。

三角基底 (複素三角基底？) \(\{e^{ix}\}\) は完全直行基底であり、ある種の \(f(x)\) が三角基底の線型結合で表せることが知られています。

フーリエ級数 (FS)

フーリエ変換の基本は周期関数です。周期 \(T\) の周期関数 \(f(x)\) は周期 \(T, 2T, \dots\) の三角基底の線型結合で表せるものとします。係数 \(c_n\) を複素フーリエ級数と呼びます:

\begin{aligned} f(x) &\sim \sum_{n=-\infty}^{\infty} c_n e^{i \frac {2 n \pi} {T} x} \\ :&= \sum_{n=-\infty}^{\infty} c_n e^{i \omega_n x} \end{aligned}

三角基底は直行基底であり、基底に対する成分 (フーリエ級数 \(c_n\)) は内積に比例します:

\begin{aligned} (f(x), e^{i\omega x}) &= (c_n e^{i \omega x}, e^{i \omega x}) \\ &= c_n (e^{i \omega x}, e^{i \omega x}) \\ &= c_n \| e^{i \omega x} \|^2 \\ &= c_n \int_{\frac{-T}{-2}}^{\frac{T}{2}} e^{i\omega x} e^{-i\omega x} \mathrm{d}x \\ &= c_n T \end{aligned}

\(c_n\) を \(f(x)\) に代入すると以下の形になります:

\[ f(x) = \sum_{n=-\infty}^{\infty} \frac {1} {T} (f(x), e^{i\omega_n x}) e^{i \omega_n x} \]

フーリエ変換 (FT)

\(T = \frac {2\pi} {\Delta \omega} \rightarrow \infty\) とすれば、非周期関数 \(f(x)\) を連続な基底ベクトル \(\{e^{i\omega x}\}_{\omega}\) で展開できます (逆フーリエ変換 (IFT)) 。

\begin{aligned} f(x) &= \sum_{n=-\infty}^{\infty} \frac {\Delta \omega} {2 \pi} (f(x), e^{i\omega_n x}) e^{i\omega_n x} \\ &= \int_{-\infty}^{\infty} \frac {\mathrm{d}\omega} {2 \pi} (f(x), e^{i\omega x}) e^{i\omega x} \\ :&= \int_{-\infty}^{\infty} \frac {\mathrm{d}\omega} {2 \pi} \mathcal{F}[f](\omega) e^{i\omega x} \end{aligned}

フーリエ変換 \(\mathcal{F}[f](\omega) := (f(x), e^{i\omega x})\) は \(f(x)\) の \(e^{i\omega x}\) 成分に相当します。指数関数の微積分は簡単なので、 \(\{e^{i\omega_n x}\}\) を基底としたのは幸先良さそうです。

三角基底による離散関数の展開

デジタル信号処理へ寄ります。ここからはビギナーズデジタルフーリエ変換および小野測器の計測コラムの em138 添付資料を参考にエアプします。

時間離散フーリエ変換

関数 \(f(x)\) を \(\tau\) の間隔で離散化し、離散関数 \(f_{\tau}(x)\) を得ます。 \(f(x)\) に周期的デルタ関数 \(\delta_{\tau}(x)\) をかけることで、 \(f(x)\) の離散化を表現します:

\begin{aligned} \delta_{\tau} (x) &:= \sum_{n \in \mathbb{Z}} \delta(x - n \tau) \\ f_{\tau}(x) &:= \delta_{\tau} (x) f(x) \end{aligned}

\(f_{\tau}(x)\) のフーリエ変換も離散化されています:

\begin{aligned} \mathcal{F}[f_{\tau}](\omega) &= (f_{\tau}(x), e^{i\omega x}) \\ &= \int_{-\infty}^{\infty} f_{\tau}(x) e^{-i\omega x} \mathrm{d}x \\ &= \sum_{n \in \mathbb{N}} f(n \tau) e^{-i \omega n \tau} \end{aligned}

さらに時間が離散化されたことから位相に周期性が生じており、 \(\mathcal{F}[f_{\tau}(x)](\omega)\) は周期 \(\frac {2 \pi} {\tau}\) の周期関数になりました (\(\mathcal{F}[f_{\tau}](\omega) = \mathcal{F}[f_{\tau}](\omega + \frac {2 \pi} {\tau})\))。

改めて \(f_{\tau}(n \tau)\) を三角基底で展開すると、次の式を得ます:

\begin{aligned} f_{\tau}(n \tau) &= \int_{-\frac {\pi} {\tau}}^{\frac {\pi} {\tau}} \frac {\mathrm{d}\omega} {2 \pi} \mathcal{F}[f_{\tau}](\omega) e^{i\omega n \tau} \end{aligned}

離散フーリエ級数 (DFS)

時間信号 \(x(t)\) の一部を時間幅 \(T\) で切り取り、 \(\tau\) の間隔で離散化したとします。この信号列を周期 \(T\) の周期関数に拡張すると、やはり複素フーリエ級数の和の形に展開できます。

\begin{aligned} x(k \tau) &= \sum_{n \in \mathbb{Z}} c_n e^{i \omega_n k \tau} \\ &= \sum_{n \in \mathbb{Z}} c_n e^{i \frac {2n\pi} {T} k \tau} \end{aligned}

\(n \in \mathbb{Z}\) とありますが、時間が離散化されたことによって位相が周期的になり、 \(x(k \tau)\) は \(\{e^{i\omega_n x}\}_{n \in [0, N - 1] \cap \mathbb{Z}}\) のみにより展開されるはずです。実際 \(n \rightarrow n + rN\) に分解して確かめられます (天才だ……):

\begin{aligned} x(k \tau) &= \sum_{n \in [0, N - 1] \cap \mathbb{Z}} \sum_{r \in \mathbb{Z}} c_{n + rN} e^{i \omega_{n + rN} k \tau} \\ &= \sum_{n \in [0, N - 1] \cap \mathbb{Z}} e^{i \omega_{n} k \tau} \sum_{r \in \mathbb{Z}} c_{n + rN} \bigg|_{c_n = 0 (|n| > N)} \\ &= \sum_{n \in [0, N - 1] \cap \mathbb{Z}} e^{i \omega_{n} k \tau} c_n \end{aligned}

上記の 2 ~ 3 行で帯域制限を設け、 \(x(t)\) が N 次の高調波成分までしか持たないとした場合、 \(\sum_{r \in \mathbb{Z}} c_{n + rN} = c_n\) から非常に簡素な式に整理できました。 N 個 (\(N = \frac T {\tau}\)) の信号 \(\{x(n\tau)\}_n\) を整理すると、以下の行列で書けます:

\begin{aligned} \begin{bmatrix} x(0) \\ x(\tau) \\ \vdots \\ x(\frac {T - \tau} T) \end{bmatrix} &= \begin{bmatrix} 1 & 1 & \dots & 1 \\ 1 & e^{i\omega_1} & \dots & e^{i{\omega_1(N-1)}} \\ \vdots & \vdots & & \vdots \\ 1 & e^{i\omega_{N-1}} & \dots & e^{i{\omega_{N-1}(N-1)}} \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \\ \vdots \\ c_{N-1} \end{bmatrix} \end{aligned}

よって時間信号 \(x(t)\) に対して 1. その一部を時間幅 \(T\) で切り抜き 2. \(\tau\) の間隔で離散化し 3. 周期 \(T\) の周期関数に拡張し 4. 帯域制限を行うと、 N 回のサンプリング結果から複素フーリエ級数が分かり、 AC の新作が発表されます。

離散フーリエ変換 (DFT)

上記の \(x(n\tau) := x_n\) に対し、なぜか改めて離散フーリエ変換 \(X_k\) を定義します (なぜ……？):

\begin{aligned} X_k &:= \sum_{n \in [0, N - 1] \cap \mathbb{Z}} x_n e^{-i \frac {2\pi} {N}k} \\ &:= \sum_{n \in [0, N - 1] \cap \mathbb{Z}} x_n W^{nk} \end{aligned}

この気持ちは勉強不足のため理解できていません。フーリエ変換の方が重要なので、単純な式にしたかった？

高速フーリエ変換 (FFT)

(2-radix) DFT の再帰的な定義

DFT の高速計算 (FFT) を小野測器の計測コラム emm140 号用から学びます。 P2 の図から汲み取れる通り、 8 点 DFT の出力 \(\{X_{8, k}\}_{k \in [0, 7]}\) は、それぞれ 4 点 DFT の和に分解できます:

\begin{aligned} X_{8,k} (\{x_k\}_{k \in [0, 7] \cap \mathbb{Z}}) &= \sum_{n \in [0, 7]} x_{n} W^{nk} \\ &= \sum_{n \in [0, 2, 4, 6]} x_{n} W^{nk} + \sum_{n \in [0, 2, 4, 6]} x_{n+1} W^{(n+1)k} \\ &= \sum_{n \in [0, 2, 4, 6]} x_{n} W^{nk} + W_k \sum_{n \in [1, 3, 5, 7]} x_{n} W^{n} \\ &= \sum_{n \in [0, 2, 4, 6]} x_{n} W^{nk} + W_k \sum_{n \in [1, 3, 5, 7]} x_{n} W^{n} \\ &= X_{4,k}({x_0, x_2, x_4, x_6}) + W_k X_{4,k}({x_1, x_3, x_5, x_7}) \end{aligned}

8 点 DFT の出力を以下の信号流れ図にまとめます。 \(\{x_n\}_n\) が上下に 2 分割されており、再帰的に \(O(N \log N)\) で計算できることが予想できます。

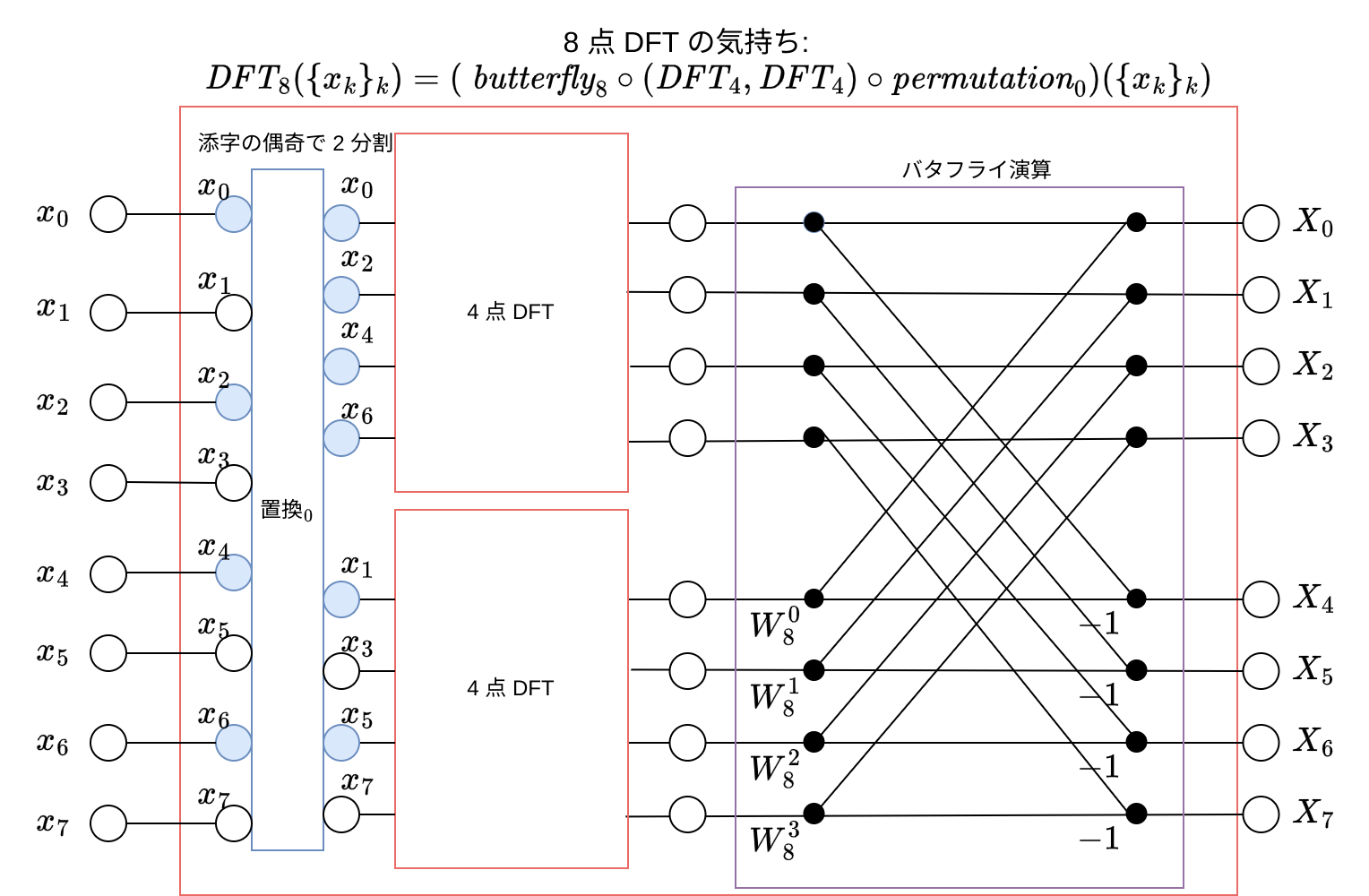
バタフライ演算の部分を丁寧に図示すると以下です。黒点を接続とし、加算器と乗算器を明示しています:

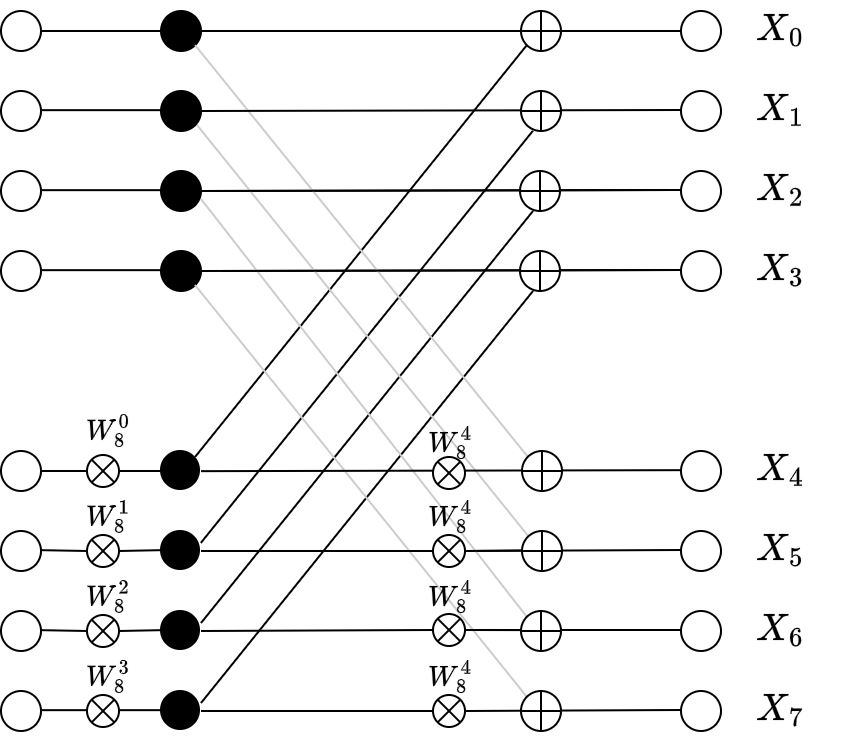
2024-05-12-butterfly-8'.png — Figure 2: 信号流れ図が読めなかったので

これを簡略化し、また \(W_8^4 = e^{i \pi} = -1\) を代入すると、前の図になります。読めないよ〜〜

バタフライ演算

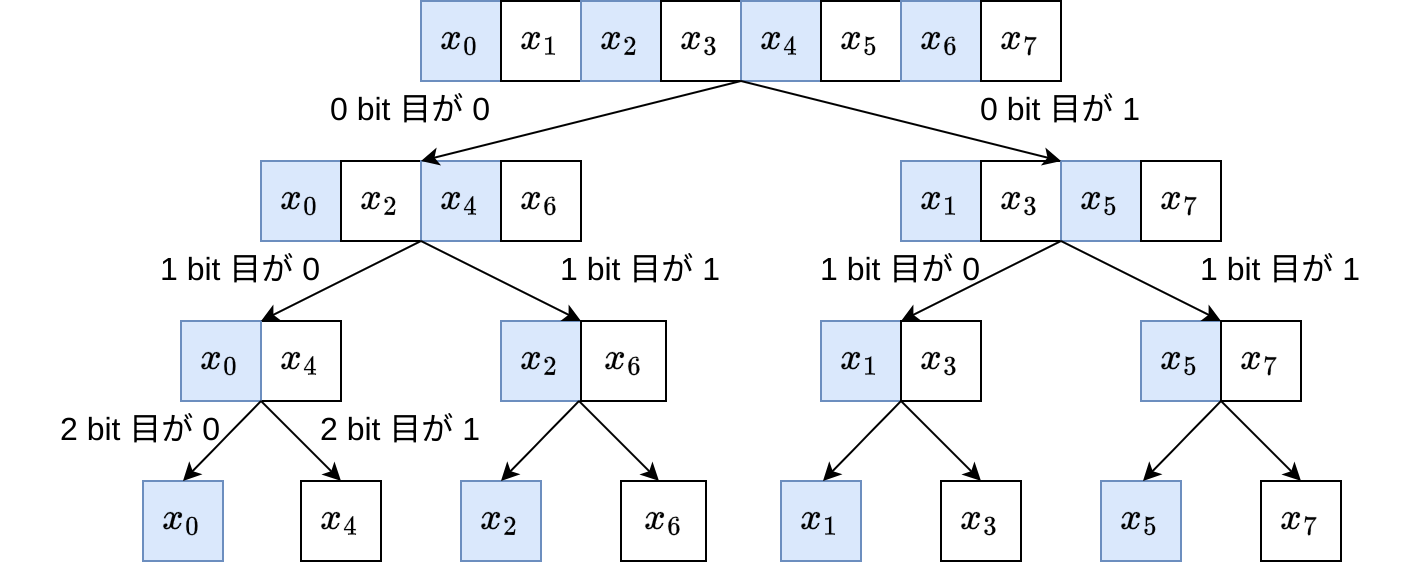
8 点 DFT を再帰的に展開すると、 \(x_0, .., x_7\) は \(x_0, x_4, x_2, x_6, x_1, x_5, x_3, x_7\) の並びになります:

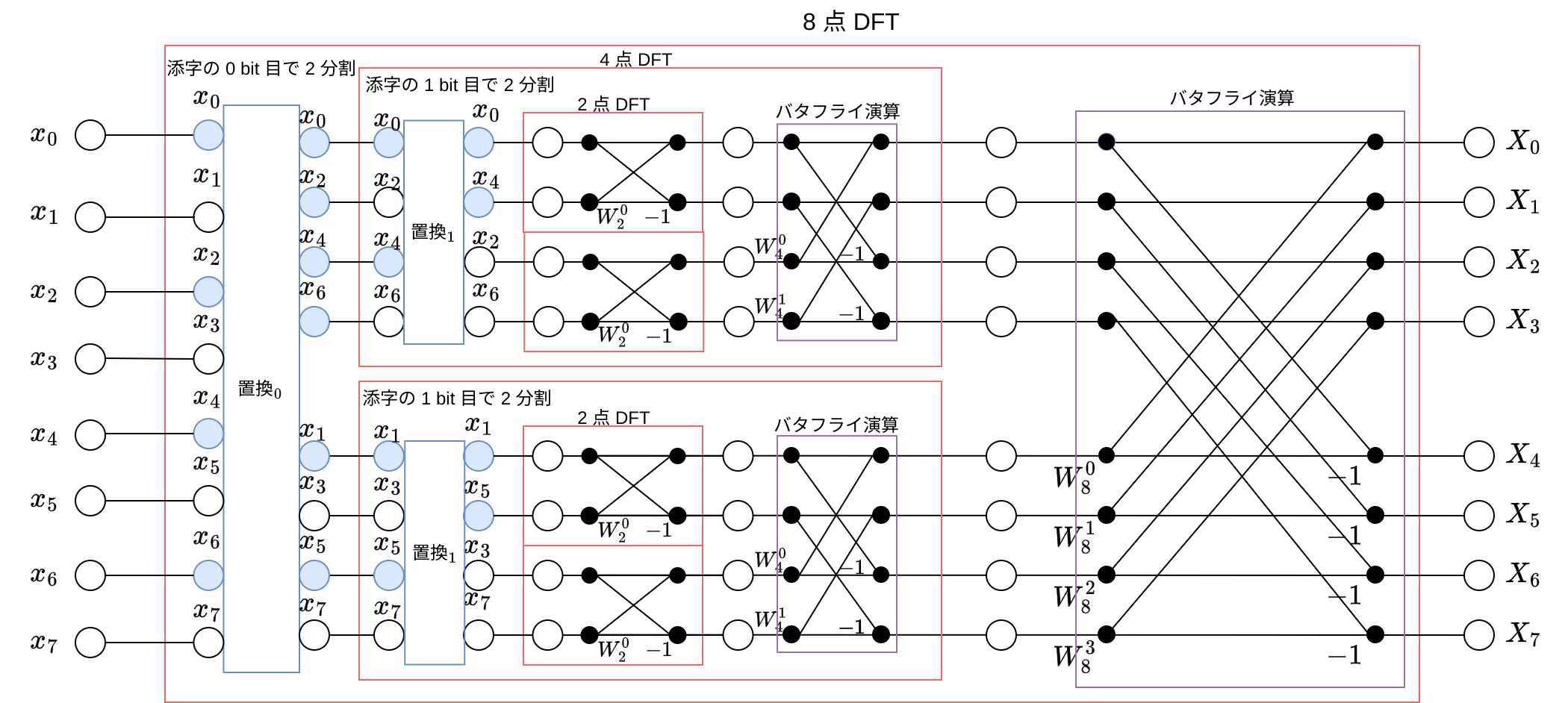
したがって以下の手順で高速に DFT を計算できます。

添字の置換を (一括して) 行う
バタフライ演算を繰り返し適用する