ARC 177 / ABC 354 / 寿司打 / Convolution (低速実装)

ARC 177

ARC 177 に参加しました。珍しく低 diff の回でした。

A 問題

貪欲です。

B 問題

貪欲です。

C 問題

貪欲です。

ABC 354

ABC 354 に参加しました。

A 問題

沼に落ちました。リストを使うべきでした。

main=interact$show.f[0..]0.read
f(i:r)a k|a>k=i|0<1=f r(a+2^i)k

数学的センスがある人は、 $\sum_{i \in [0, k-1]} 2^i = 2^k-1$ による簡潔な解答になるようです。

待って、これは何ですか (exponent) ??　地球は今日も美しい……

B 問題

ソートして指定番目のデータを抜き出します。

import Data.List
main=interact$(g<*>sort.f<*>(0%).tail).words
s%[]=s
s%(_:b:r)=s+read b%r
f[_]=[]
f(_:n:r)=n:f r
g(n:_)x t=x!!(t`mod`read n)

Applicative style が精一杯です。いずれコードゴルフ記事を書けるほどの実力が……無くてもいいですね。内輪ネタ過ぎますか。

C 問題

平面走査の一種として捉えると、 1 回の走査で答えを出したくなります。

状態を持って mapMaybe がしたかったので、 State モナドを使用しました。 これが模範的な Haskell であるとは決して思いません が、自分の中では王道です。

solve :: StateT BS.ByteString IO ()
solve = do
  !n <- int'
  !acs <- U.replicateM n ints2'

  let !acs' = U.modify (VAI.sortBy (comparing (Down . fst . snd))) $ U.indexed acs
  let !res = (`evalState` (maxBound @Int)) $ (`U.mapMaybeM` acs') $ \(!i, (!_, !c)) -> state $ \acc ->
        let !acc' = min acc c
         in if c <= acc then (Just i, acc') else (Nothing, acc')

  printBSB $ G.length res
  printVec $ U.map (+ 1) $ U.modify VAI.sort res

State 以外で状態を持つ方法としては、たとえば以下があります。どれも厳しい要求で、 Haskell には崖があると思います。

• IORef に状態を載せつつ mapMaybeM でループする
  これが無難です。
• IORef に状態を載せつつ concatMapM でループする
  これもいけますね。
• mapAccumL で [Maybe Int] に写し、後で catMaybe する
  アリです。
• foldl' で状態を持ってループしつつ、リストに出力を溜める (後で reverse する)
  動けば良かろうなのだ！
• 再帰関数で状態を持つ
• 他にも色々あると思います

初心を思い出しました。解けて良かった…….

D 問題

Imos 法で解くのが典型です。解けて良かったシリーズに入りました。

入力は x1 y1 x2 y2 形式のようです。問題文からは (A, B) が (x, y) なのか (y, x) なのか分からない点が改善の余地ありと思います。

同種の問題で高難度版としては ABC 269 F - Numbered Checker があります。

E 問題

集合 DP で解くのが典型です。遷移先に 1 つでも後手必勝のケースがあれば先手の勝利です。

解けて良かったシリーズでした。

F 問題

Upsolve します。やはり F が解けないとな〜……

Misc

AI で典型問題が解ける点が徐々に物議を醸しています。自分程度の実力でも周囲と相対化される (極端に弱かったりそこそこ強かったりする) のが面白かったわけですが、徐々に元の曖昧な世界へ戻っていくんだなと思いました。

寿司打

寿司打 で 20,700 点を記録しました。元々タイピングが遅かったこともあり、ささやかな栄光でした。

次は 16 キーのキーボードをゲットして、同じ成績を目指してみたいです。誰か氏〜

Convolution (低速実装)

前回の日記で FFT の概要と計算方法を理解しました。今回は NTT (数論変換) と convolution (合成積) の概要を学び、 Haskell で実装します。

FFT が載っている CS の本として、 Introduction to Algortihms や Modern Computer Algebra があるようです。そっちを読めば良かったかも。

※ 今回も自分専用のノートです。

地固め

前回の疑問 (DFT)

離散的フーリエ級数が自然に求まるのに対し、なぜ改めてスケール違いの計算式 (DFT) を再定義するのか疑問に思いました (前回の日記) 。

大した理由は無さそうでした。実際、 DFT の定義式が流派によって異なる ようで、正規化パラメータにはブレがあるようです。今回は以下の式を採用します。

$$\begin{aligned} W_N^k &:= e^{-i\frac{2\pi}{N}k} \\ X_N^k &:= \sum_{n \in [0, N - 1] \cap \mathbb{Z}} x_n W_N^{nk} \\ x_k &:= \frac {1} {N} \sum_{n \in [0, N - 1] \cap \mathbb{Z}} X_n W_N^{-nk} \end{aligned}$$

TODO : 周期の規格化

$W_N^k$ の定義には周期 $T$ (または周波数 $\omega = \frac {2\pi} {T}$) がありませんでした。時間の規格化は係数に吸収されている？　勉強不足です……

FFT と線形代数の関連

DFT は基底変換だと思いました。 FFT を要約すると、『基底変換の際に変換先の基底として 1 の N 乗根を選んだ場合、分割統治によって $O(N \log N)$ で変換先の成分を計算できる』と言えそうです。 NTT への拡張を予感させます。

DFT から NTT へ

NTT (数論変換)

FFT は精度が悪く 、競技プログラミングでは NTT (数論変換) の方が出題されるようです。

結論

$W_N$ を $1^{-\frac 1 N}$ (1 の N 乗根の逆数) とすれば、 $\bmod p$ の世界でも FFT を実施できます。 $1^{\frac 1 N}$ は以下の通り求まります。

$g$ が『原始根』であるとき、Fermet の小定理から $1 / 2^m \pmod p$ が分かります:

$$\begin{align} g^{p-1} &= 1 \pmod p \\ (g^{p-1/{2^m}})^{2^m} &= 1 \pmod p \end{align}$$

$g^{p-1/2^m}$ を 2 乗していくと、 $1/2^m, .., 1/4, 1/2$ がすべて求まります。また特に 998244353 に対する原始根 g は 3 です (WolfarmAlpha にて PrimitiveRoot[988244353] の答えを見るか、計算式を調べて実装します)。

理論 (未習得)

原始根って、何ですか……？　理論習得のために 【NTT（数論変換）入門（２）】NTT（数論変換）編 - Zenn の理解を目標にします。この記事を理解できないのは『巡回群』に馴染みが無いためで、つまり『群論への第一歩』を読んでいないためと思います。

まずは『群論への第一歩』を読もうと思います。しかし、学部レベルの勉強をもっと真っ当にやっていれば、もっと直接的に役立ったのかもしれません。

Convolution (畳み込み、合成積)

いよいよ目的の関数が見えて来ました。 Haskell の文脈では畳み込み = fold のため、ここでは合成積を convlution の訳語とします。

連続関数の合成積

周期 $T$ の連続関数 $f(x)$, $g(x)$ に対し、 合成積 $(f * g)(x)$ を次式で定義します:

$$(f * g)(x) := \int_{-\frac{T}{2}}^{\frac{T}{2}} f(\tau)g(x-\tau)\mathrm{d}\tau$$

合成積に対するフーリエ変換は、フーリエ変換の積に分解できます:

$$\begin{align} ((f * g)(x), e^{i\omega x}) &= \int_{-\frac{T}{2}}^{\frac{T}{2}} (f * g)(x) e^{-i\omega_n x} \mathrm{d}x \\ &= \int_{-\frac{T}{2}}^{\frac{T}{2}} (\int_{-\frac{T}{2}}^{\frac{T}{2}} f(\tau)g(x-\tau)\mathrm{d}\tau) e^{-i\omega_n x} \mathrm{d}x \\ &= \int_{-\frac{T}{2}}^{\frac{T}{2}} (\int_{-\frac{T}{2}}^{\frac{T}{2}} f(\tau)g(x-\tau)\mathrm{d}\tau) e^{-i\omega_n \tau} e^{-i\omega_n (x-\tau)} \mathrm{d}x \\ &:= \int_{-\frac{T}{2}}^{\frac{T}{2}} (\int_{-\frac{T}{2}}^{\frac{T}{2}} f(\tau)g(y)\mathrm{d}\tau) e^{-i\omega_n \tau} e^{-i\omega_n y} \mathrm{d}y \\ &= \int_{-\frac{T}{2}}^{\frac{T}{2}} f(\tau) e^{-i\omega_n \tau} \mathrm{d}\tau \int_{-\frac{T}{2}}^{\frac{T}{2}} g(y) e^{-i\omega_n y} \mathrm{d}y \\ &= \mathcal{F}(x)[\omega] \mathcal{F}(g)(x) \end{align}$$

積分 2 つにバラしているところが納得行きません。 $y = y(\tau)$ なので $\tau$ の積分から分離できないと思いますが……？　積分の基礎知識が足りないようです。

離散関数の合成積

数列を $f(x) = \sum_i \delta(i - x) a_x$ のように離散的な関数として見ることで、次式の合成積が得られると解釈しました:

$$\begin{align} a &:= (a_0, a_1, .., a_{n-1}) \\ b &:= (b_0, b_1, .., b_{m-1}) \\ (a * b)_n &:= \sum_{t \in [0, n] \cap \mathcal{Z}} a_t b_{n - t} \end{align}$$

数列の例としては多項式の係数があります。多項式の積の係数部分は合成積で表されます。この辺りは 高校数学の美しい物語 の図解が良かったです。

$$\begin{align} \mathbb{a} &:= \sum_i a_i x^i \\ \mathbb{b} &:= \sum_i b_i x^i \\ (\mathcal{a} \mathbb{b})_n &= (a * b)_n x^n \end{align}$$

よって $\mathbb{a} * \mathbb{b} = \mathcal{F^{-1}}(\mathcal{F}(\mathbb{a}) \mathcal{F}(\mathbb{b}))$ により、多項式の積が $O(N \log N)$ で求まります。

まとめ

多項式の積を計算する際に、 1 の N 乗根の基底に基底変換し、分割統治で成分を求めた上で、元の基底に対する成分を計算することにより、 $O(N \log N)$ で計算できます。

実装

改めて DFT, IDFT の式を眺めます。

$$\begin{aligned} \mathcal{F}&: \{x_i\}_i \mapsto \{X_i\}_i \\ \mathcal{F^{-1}}&: \{X_i\}_i \mapsto \{x_i\}_i \\ X_k &:= \sum_{n \in [0, N - 1] \cap \mathbb{Z}} x_n W_N^{nk} \\ x_k &:= \frac {1} {N} \sum_{n \in [0, N - 1] \cap \mathbb{Z}} X_n W_N^{-nk} \end{aligned}$$

FFT の図は前回同様で、 IDFT の計算方法もこの図から分かります:

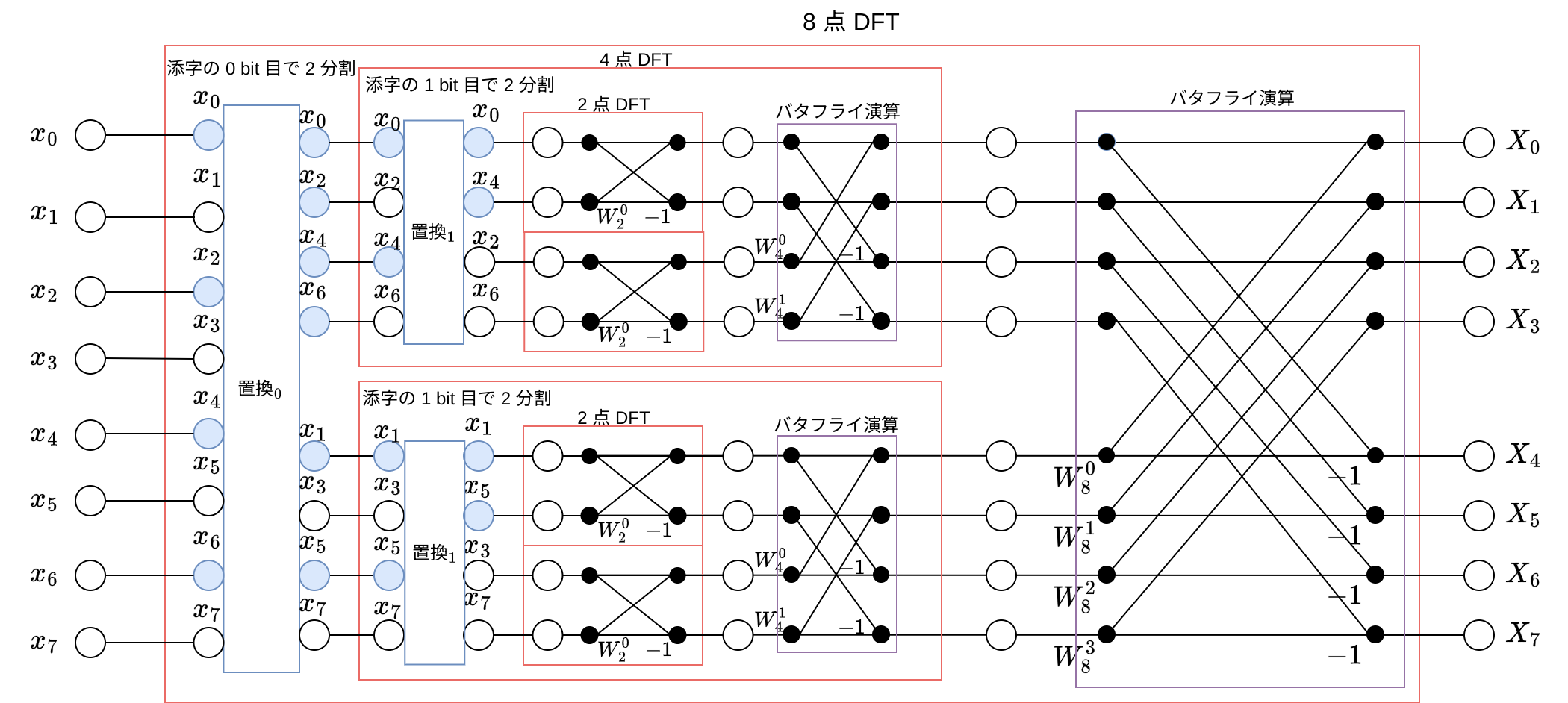
以上を元に、各種関数を実装しました:

• bitRevSort: 引数並び替えの部分
  絶対にやってはいけないビット反転 を参考に実装しました。逆変換は bitRevSort 自身です。
• butterfly: $\mathcal{F}(\mathbb{a})$ の内、引数の並び替え以外の部分
  上図の通り実装します。ただし $W_N^i := (1^{-\frac i N}) \pmod p$ とします。
• invButtefly: $\mathcal{F^{-1}(\mathbb{a})}$ の内、引数の並び替え以外の部分
  上図で右から左へ逆向きに回路を辿る式を考えて実装します。
• convolute: $\mathbb a * \mathbb b = \mathcal{F^{-1}}(\mathcal{F}(\mathbb{a}) \mathcal{F}(\mathbb{b}))$
  式の通り実装します。

詳細は cojna/iota の Math.NTT を参考に実装しました。ただし iota においては bit 反転によるソートを実施していない？のか、計算方法に違いがあります。

verify

まだまだ低速ですが、 convolute を使って行きます。

• Convolution - Library Checker
  convolute そのものの問題です。
• ACL Practice Contest F - Convolution
  Library Checker の問題と同じです。テストケースは弱め (?) です。
• AtCoder Typical Contest 001 C - 高速フーリエ変換
  よく考えると合成積そのものな問題です。テストケースが弱いので解く必要はありませんが、スライドが良いと思います。
• 典型 90 問 065 - RGB Ball 2 (★7)
  いずれ見ます……

中国剰余定理 (CRT / Garner's algorithm)

• PAST 10 N - 400億マス計算
  2 つの項の和について考える時、和を指数部に持っていくことで合成積に持ち込める。天才ですね。ただし $\bmod$ を取らない？合成積 (convolution_ll 相当) が必要で、そのために中国剰余定理 (CRT / Gerner's algorithm) を使っているようです。

convolutin_ll (convolution.hpp)

aclのconvolution_llってどうやって実装してるんだと思ったが3本計算してCRTで復元してるのか

— だうなー (@downerkei) March 25, 2024

CRT は理解していませんが、 ACL を写経して AC しました。解けるから今はヨシ……！

今後

僕の convolution は、今より 10 倍速くなりそうです。将来的には 爆速なNTTを実装したい - 競プロ備忘録 などを参考に高速化が必要です。

関連

• 2023年の Linear Haskell で純粋・並列 FFT を実装する──「Haskell は Rust になれるのか？」補遺
• FFT のハードウェア実装？

Misc

SparseGraph から頂点の型パラメータを削除

SparseGraph i w においては頂点の型 i (Index i) を抽象化していましたが、 Int 型に固定しました。 (x, y) のように成分に分けた API が欲しければ、都度グラフをラップした関数を作成します。