ABC 358 / Z Function / Suffix Array / SKK

Jun 16, 2024

ABC 358

ABC 358 に参加しました。

問題	A 問題	B 問題	C 問題	D 問題	E 問題	F 問題	G 問題
予想	1	2	500	900	1,800	1,600	2,400
実際	11	43	273	393	1,397	2,098	1,737

Table 1: Diff 予想

A 問題

interact の罠がよく分かる問題です。入力ファイルの末尾に改行文字があります。

main=interact b;b"AtCoder Land\n"="Yes";b _="No"

注意点として改行文字 (LF) が 2 バイト (CRLF?) になりがちです。

AtCoderでコードゴルフをするにあたって
submitページから直接提出すると、改行文字は2Byteとカウントされます。

; で区切ったほうが面倒がありません。 Kotatsugame さんは改行文字を 1 バイトにして提出するブラウザ拡張を使っています。

B 問題

scanl の問題です。

main=interact$unwords.map show.f.map read.words;f(n:a:t)=tail$scanl(\x y->max x y+a)0 t

コードゴルフが目的でなければ scanl' を使います。 vector パッケージにおいては postscanl' を使えば tail する必要がありません。

C 問題

Bit 全探索と bitset の問題でした。 Bit mask の和を取るときは、 sum ではなく foldl' (.|.) (0 :: Int) を使わねばなりません……

D 問題

2 つのリストをソートしてマッチさせて行くのが良さそうです (cojna さんの提出) 。

僕は multiset でズルをしてしまいました。

E 問題

DP でした。選んだ文字の長さに注目し、その内訳を忘れ去ることで、状態数を大幅に削減し緩和が効きます。良問ですね。

Upsolve します。

Z Function

文字列に苦手意識があります。特に文字列のアルゴリズムは全容が見えて来ません。困難は実装せよということで、 Algorithms for Competitive Programming を写経しました。

Z-function - Algorithms for Competitive Programming

このサイトは初見に厳し目ですが、読めば分かるように書いてあって高印象……好印象です。以下は自分用メモです。

$O(N^2)$ 実装

Z 関数 (配列) の定義を以下とします:

$z[i] := \mathcal{lcp}(s[0:], s[i:])$

愚直に計算します:

-- | \(O(\max(N, M))\) Longest common prefix calculation. \(z[0] := |s|\).
lcpOf :: BS.ByteString -> BS.ByteString -> Int
lcpOf bs1 bs2 = length . takeWhile id $ BS.zipWith (==) bs1 bs2

-- | \(O(N^2)\) Z function calculation. \(z[0] := |s|\).
zOfNaive :: BS.ByteString -> U.Vector Int
zOfNaive bs = U.generate (BS.length bs) z
  where
    -- z 0 = 0
    z i = lcpOf bs (BS.drop i bs)

$O(N)$ 実装

$s$ と接尾辞 ( $s[1:], s[2:], \dots$ ) のマッチの内、最も右端までマッチした範囲を z-box と呼んで保持します。 z-box 内の $i$ に対する $z[i]$ の計算には $z[i'] (i' < i)$ の計算結果を利用できます:

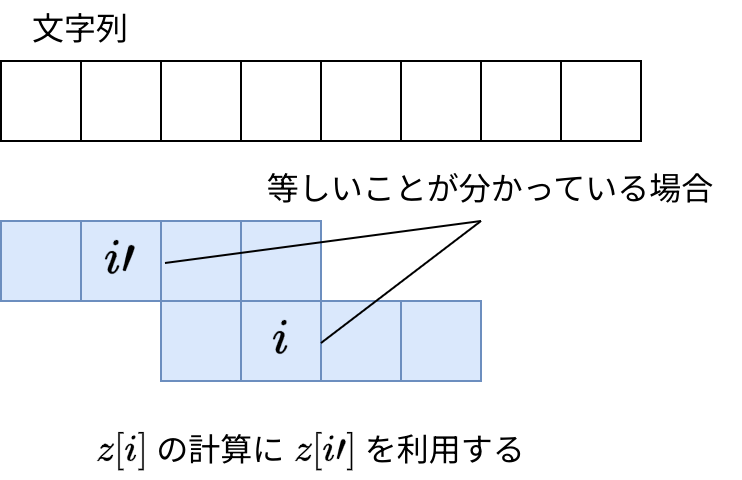
実装中は z-box を状態に持って constructN したくなりました。しかし constructN が引数に取るのは純粋関数です。やはり cojna さんの実装と同様に可変配列を手動管理しました。僕の実装 (ZFunction.hs)

$O(N)$ になるお気持ち

z-box の右端は単調増加します。 LCP の trivial 解による文字比較の回数は、マッチした場合・マッチしなかった場合がそれぞれ高々 n 回となります。よって $O(n)$ で計算できています。そんなお気持ちです。

Library Checker

Z Algorithm - Library Checker が 22 ms でした。さすが $O(N)$ です。

まだ使い方は知らず、エアプです。

Suffix array

Suffix Array - Algorithms for Competitive Programming

ACL I - Number of Substrings で立ちはだかるデータ構造です。以下は自分用メモです。

$O(N \log N)$ 実装

Suffix Array - Algorithms for Competitive Programming

写経しました。分割された困難のメモです:

文字列 s の i 番目の suffix とは (復習)
例: s := abc に対する [abc, bc c] !! i です。
メタ文字 $
長さの異なる文字列の辞書順比較は、『最小の文字』を表すメタ文字 $ を補完して解釈できます。たとえば ab と abcd の比較は ab$$ < abcd です。
p[i]: 計数ソート (counting sort) による順列の生成 (sa の生成過程)
等しい部分列の出現回数を記録し、累積和を取ります。累積和を基に、それぞれの部分列に 0 ~ (n - 1) の番号を割り当てます (順列を生成します) 。
c[i]: Class, equivalent class
等しい部分列に等しい値 (辞書順で小さいものから 0, 1, 2..) を与えます。以降は元の文字列を忘れ、 class をベースにソートします。
ダブリング
文字列の末尾にメタ文字 $ を挿入します。これに対し長さ $2^i (i \in [0, 1, .., \lceil \log_2 N \rceil])$ の循環部分列のソートを求めることで、 suffix array が求まります。
賢いソート
ダブリング時のソートは工夫により $O(N)$ になります。接尾辞の長さを 2 倍にするとき、右側半分でのソートは既に実施されているため、左側半分で stable sort すれば良いです。計数ソートは stable sort になるように注意します (添字の割当の際に reverse します) 。

積み重ねが凄くて面白いですね。

Library checker

Suffix Array - Library Checker が 234 ms でした。 $O(N)$ 実装は 2 ~ 7 倍速くなります。

$O(N)$ 実装 (スキップ)

SA-IS (suffix array induced sorting) が $O(N)$ で強いらしいです。 $O(N)$ でなければ間に合わない問題もしばしばあるようですが、大変らしいので飛ばします。

LCP 配列 (Kasai's algorithm)

Suffix array と LCP 配列を併用すると、 suffix trie よりも効率が良いと評判のようです。 Suffix trie のことは知らないので、 trie との関連付けは一旦忘れることにします。

LCP 配列とは

多数の $lcp(s[sa[i]:], s[sa[j]:])$ クエリへの応答を考えます。 $s[sa[i]:], s[sa[j]:]$ を直接比較して LCP を求めたいところですが、任意の $i, j$ に対して LCP を高速で求める工夫が必要です。

ここで $\mathcal{lcp}[i] := \mathcal{lcp}(s[sa[i]:], s[sa[i+1]:])$ を用いて $\mathcal{lcp}(i, j) = \min \{ \mathcal{lcp}[k] ) \}_{k \in [i .. j)}$ のようです。 $\mathcal{lcp}$ 配列の添字が辞書順ソート後の接尾辞列に対する添字であることを考えると、 $s[sa[i]:]$ から $s[sa[j]:]$ までの間は、徐々に $s[sa[j]:]$ に向かって文字列が編集されていくように見えます。実際 $\mathcal{lcp}(s[sa[i]:], s[sa[k]:])$ は $k$ が増加するにつれて単調減少します。ここで $k \in [i .. j - 1]$ の範囲で min 演算子で LCP を畳み込むことで $lcp(s[sa[i]:], s[sa[j]:])$ の計算を代替できるようです:

                      LCP      LCP (畳み込み)
1:   a b a b a b
     *-*-*-*          4        4
2:   a b a b c d
     *                1        min 4 1 = 1
3:   a c a b c d
     *-*-*-*-*        5        min 1 5 = 1
4:   a c a b c e

Listing 1: min で LCP を畳み込む

(証明が欲しい)

また重要な事実として suffix array 上で隣接した 2 項の LCP が最も大きく、間隔を広げると LCP は広義単調減少します。このことから次の Kasai's algorithm を導けます。

Kasai's algorithm ( $O(N)$ )

LCP 配列生成の方法は $O(N)$ Kasai's algorihm を採用します。より高速な実装も多数ある (LCP配列の構築アルゴリズムたち) ようですが、 $O(N)$ の時点で十分高速です。

Kasai's algorithm では最長の suffix から順に LCP 配列の値を確定させます。 (元の添字 → ソート後の添字) を $\mathcal{sa}^{-1}$ として

\begin{aligned} \mathcal{sa}[\mathcal{sa}^{-1}[i]] &:= i \\ \mathcal{lcp}[\mathcal{sa}^{-1}[i]] &:= \mathcal{lcp}(s[i:], s[\mathcal{sa}[\mathcal{sa}^{-1}[i]+1]:]) \\ \mathcal{lcp}[\mathcal{sa}^{-1}[i+1]] &\ge \mathcal{lcp}[\mathcal{sa}^{-1}[i]] - 1 \\ \end{aligned}

3 行目は $s[(i+1):], s[(\mathcal{sa}^{-1}[i]+1]+1):]$ が存在し $\mathcal{sortedIndexOf}(s[(i+1):]) < \mathcal{sortedIndexOf}(s[(\mathcal{sa}^{-1}[i]+2):])$ から前項 (LCP の min 畳み込み) によって証明できます。

ACL / Library Checker

ユニークな部分列の数を数える問題です。ここでも suffix array 上で隣接する 2 項間の LCP 値が最大であることを踏まえて、 $\mathcal{sa}[i]$ と結合できる prefix (空でも良い) を重複無く数える式を考えると $\sum\limits_i {(n - \mathcal{sa}[i] - \mathcal{lcp}[i])} = n^2 - \frac {n (n - 1)} {2} - \sum\limits_i \mathcal{lcp}[i]$ が導かれます。

なぜ $\mathcal{lcp}[i]$ を引けば良いのか。それは prefix の suffix + 対象の suffix が他の suffix と一致することを避けるためのようです。この辺も難しい。。

感想

ACL の文字列データ構造 (Z Funciton および Suffix Array) を実装しました。最大流とか遅延セグメント木に比べれば簡単な方ですが、使い方が見えない点が苦痛です。幸いプログラミングにおいては困難は実装せよで理解が進むため、なんとか喰らいつくことができました。

Haskell

醜い Haskell のフォーマット

Z function の愚直実装は美しいフォーマットでした。 gksato さんの提出から学んだことですが、 . を使うとインデントが減ります:

saOfNaive :: BS.ByteString -> U.Vector Int
saOfNaive bs =
  U.convert
    . V.map fst
    . V.modify (VAI.sortBy (comparing snd))
    $ V.generate n (\i -> (i, BS.drop i bs))
  where
    n = BS.length bs

逆に $ を使うと ormolu がインデントを重ねます。 $ を使ってダサくなりましょう:

saOfNaive :: BS.ByteString -> U.Vector Int
saOfNaive bs =
  U.convert $
    V.map fst $
      V.modify (VAI.sortBy (comparing snd)) $
        V.generate n (\i -> (i, BS.drop i bs))
  where
    n = BS.length bs

Listing 2: ダサい Haskell

QuickCheck alternatives?

今回の QuickCheck も、単なるランダムテストで愚直解と高速解を比較しています。ランダムではなく、小さい入力を全点チェックすれば良い (exhaustive test を実施すれば良い) 気もします。

肝心の smallcheck が obsolute となっていました。
falsify は smallcheck の README からリンクされていますが、 exhausive test を強調していません。新しい仕組みをウリにしています。 tasty 版はありません。
hedgehog は quickcheck とほぼ同数の star を持つ歴史有りそうなライブラリで、 tasty-hedgehog もあります。

これは QuickCheck 上で exhaustive test を実施する方法を調べたほうが良さそうです。

Misc

`nerd-icons.el`

Emacs ではアイコンレスなターミナル人生を歩んで来ましたが、 nerd-icons.el により華やかになりました。この 1 週間、何度見ても嬉しいです。

neotree に関してはこちらの PR がマージされれば、ほぼ out-of-the-box でアイコン表示できるようになるはずです。黄金期！ Emacs の時代は何度来ても良いですからね。

内なるクソリプの衝動

X で Emacs の画像を送りつけてしまいました。しばらく控えます……

AtCoder-JOI

半年間レーティングが上がらず苦しんでいます。過去のレーティングの上げ方はこんな感じです:

レーティング	レーティングを上げた (つもりの) 方法
灰色	典型 90 問の ★ 2, ★ 3 を解く
茶色	平日に問題を解く
緑色	水 diff を 100 問解く

適切な時期に適切な問題を解くのが効く……と思いこんでいます。

現在の僕は JOI の ★ 4 〜 ★ 6 を解くのが良い と助言を頂いたので、素直に取り組んでみます。ありがたい……！ AtCoder-JOI をあたります。

`oj t -M diff-all`

naoya さんの ABC357振り返りで oj の side-by-side diff を知りました。 ~~ずるいや……！~~

Nix 上の環境構築を確認中……

`skk-tutorial`

日本語入力には、やはり SKK が良いらしいです。 macOS の方で DDSKK の skk-tutorial をやっています。 140 問くらいあるんですよね。

Q3-4 左手の小指を SHIFT で酷使したくありません。

これを見ると親指キーを SKK 専用のキーにするのが良いとあります。僕の Keyball には既に Enter キーや IME on, IME off が親指にあり、操作感を崩さずに移行するのが良さそうです。

Misc of misc

危機感さんアニメ化
めでたい 🎉
宮崎雄也と音楽の話 1,000 subscribes 突破
めでたい 🎉
Elin ベータテスト開始
めでたい 🎉