AHC 034
AHC 034 に参加しました。グリッドに +-100 の値が設定されており、効率良く 0 に均す問題でした。いつも通り適当にパスを作ってうろちょろすることしかできず、成長の仕方が分かりません。
yosupo さんが 1 位でした。かっこいい。 トヨタ自動車プログラミングコンテスト2024#6(AtCoder Heuristic Contest 034) 解法 - よすぽの日記
ABC 359
ABC 359 に参加しました。
| 問題 | A 問題 | B 問題 | C 問題 | D 問題 | E 問題 |
|---|---|---|---|---|---|
| 予想 | 10 | 300 | 1,300 | 1,100 | 1,500 |
| 実際 | 10 | 27 | 828 | 1381 | 1275 |
A 問題
なんと文字検索の問題でした:
main=interact$show.length.filter(=='T')
B 問題
\(i \in [0, 2n - 3]\) の範囲で見ます:
main=interact$show.sum.f.map read.words;f(n:x)=[1|i<-[0..2*n-3],x!!i==x!!(i+2)]]
zipWith を使うが上手い方法ですね:
B を zipWith3 で華麗に解いたのでボーナス点ください pic.twitter.com/zkJvzLdVBy
— naoya (@naoya_ito) June 22, 2024
C 問題
無理過ぎる……
D 問題
直前 K 文字の状態を持って DP します。 \(K\) 文字目までと \(K\) 文字目以降で処理が変わるのが厄介なところです。
E 問題
\(i\) 番目の壁を乗り越えるためには、 \(j \le i (\forall k \in [j, i], A[k] \le A[i])\) を高さ \(A[i]\) まで埋める必要があります。また \(j - 1\) 番目の壁を乗り越えるためには、 \(dp[j - 1]\) の水が必要です。
DP 解法 1. [x] 区間 Max の 2 分探索
Max モノイドのセグメント木を持ちます。上記の \(j\) を 2 分探索によって発見します。計算量は \(O(N \log^2 N)\) ですが、簡単で良い方法だと思います。
DP 解法 2. [ ] 区間 Max を伸ばしていくモノイド
区間 Max をどこまで伸ばしていけるか判定するためのモノイドを作成します。計算量は \(O(N \log N)\) ですが、真横のモノイド同士しか結合できないなど、細かい判定がかなり大変です。
DP 解法 3. [ ] 遅延伝播セグメント木を用いたシミュレーション
同様に、重い方針だと思います。
別解. [ ] スタックを持ってシミュレーション
なるほど。ここでスタックは償却計算量 \(O(1)\) (1 回のクエリで最大 1 つのみ要素が追加され、それぞれの要素は最大 1 度のみ使用される) であり、 \(O(N)\) で解けるみたいです。
アライグマ「E問題は、最大長方形問題みたいにスタックを使うのだ! 前の壁より高い壁が出てきたら、前のゾーンも高い壁の高さまで行かないと超えられないから、今まで越えた壁の高さと位置をスタックで持ちながら計算すればいいのだ!」 pic.twitter.com/zipQFclCgL
— 競技プログラミングをするフレンズ (@kyopro_friends) June 22, 2024
F 問題
難しそうですが……。
Floor sum (unsigned)
AtCoder Library Practice Contest (ALPC) を埋めました。最後に残った問題が floor_sum でした。 floor_sum の解説は、 【math編】AtCoder Library 解読 〜Pythonでの実装まで〜 が良かったです。この記事の図を写経して理解しました。
以下は 100% 自分用のメモです。
TODO: 誤記修正 (多数)
概要
Floor sum は 1 次関数 \(y(x) := \frac {ax + b} {m} (a, b \in \mathbb{Z}_{\ge 0}, m \in \mathbb{N})\) の下側にある格子点の数を高速で数えるアルゴリズムです。具体的には、 \(S := [(y, x) | x \in [0, n), y \in (0, y(x)]]\) 中の格子点の数を \(O(\log aN)\) で求めるアルゴリズムです。
考察
\(S\) を 3 つに分けて計算します。
\(S_1, S_2\)
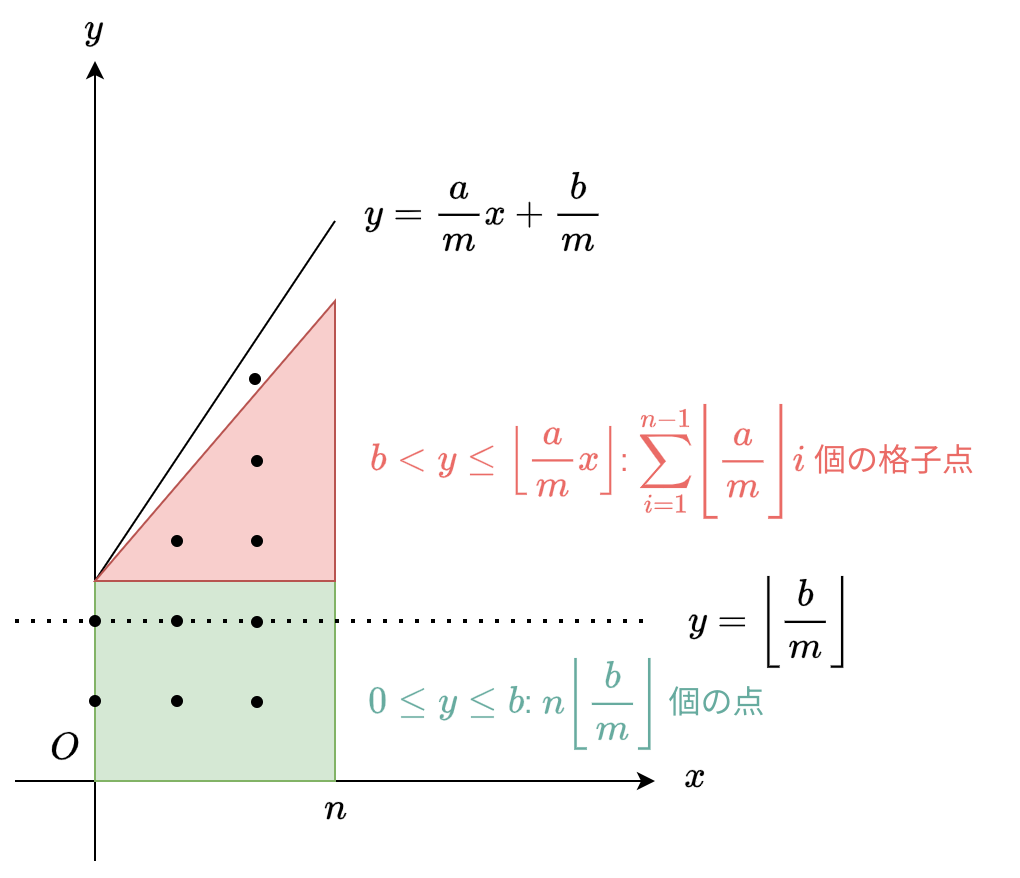
- x, y の変域は半開区間であるため、 S の下端と右端には格子点がありません。
- 緑箇所 \(S_1 := S \cap y \le \frac {b} {m}\) 中の格子点の数は \(n \lfloor \frac b m \rfloor\) です。
- \(\lfloor \frac b m \rfloor\) は \(y(x)\) の y 切片の整数部分です。
- \(y \gt 0\) に注意します。
- \(\lfloor \frac b m \rfloor\) は \(y(x)\) の y 切片の整数部分です。
- 赤色箇所 \(S_2 := S \cap y \gt \frac {b} {m}\) 中の格子点の数は \(\sum\limits_{i=1}^{n-1} \lfloor \frac a m \rfloor\) i です。
- \(y \gt \frac {b} {m}\) より \(S_1\) と \(S_2\) は共通部分を持たず、格子点のダブルカウントを避けられます。
- \(y = \lfloor \frac {a} {m} \rfloor\) は \(y(x)\) と共通の y 切片を持つ傾きが整数の直線であって傾きが最大のものです。 \(y \ge 0\) を保つ限り \(y = \frac {a} {m}\) から \(y = x\) を引ける回数が \(\lfloor \frac a m \rfloor\) であるとも言えます。
- y 方向の変域 \((\frac b m, \frac b m + \lfloor \frac a m \rfloor x] (x \in \mathbb{N})\) の大きさは、たとえるならば \(整数値 - \mathcal{eps}\) です。よって \(S_2\) 中の格子点の数は y 切片の値によらず常に \(\sum\limits_{i=1}^{n-1} \lfloor \frac a m \rfloor\) です。
- y 方向の変域 \((\frac b m, \frac b m + \lfloor \frac a m \rfloor x] (x \in \mathbb{N})\) の大きさは、たとえるならば \(整数値 - \mathcal{eps}\) です。よって \(S_2\) 中の格子点の数は y 切片の値によらず常に \(\sum\limits_{i=1}^{n-1} \lfloor \frac a m \rfloor\) です。
- \(y \gt \frac {b} {m}\) より \(S_1\) と \(S_2\) は共通部分を持たず、格子点のダブルカウントを避けられます。
\(S_3\)
残る \(S_3 := [(y, x) | x \in [0, n - 1], \lfloor \frac {a} {m} \rfloor \frac {b} {m} \lt y \le y(x)\) を考えます。 \(y' := y - \lfloor \frac b m \rfloor\) にフォーカスします。このとき元の直線は \(y' = \frac {a} {m} + \frac {b \% m} {m}\) となります。
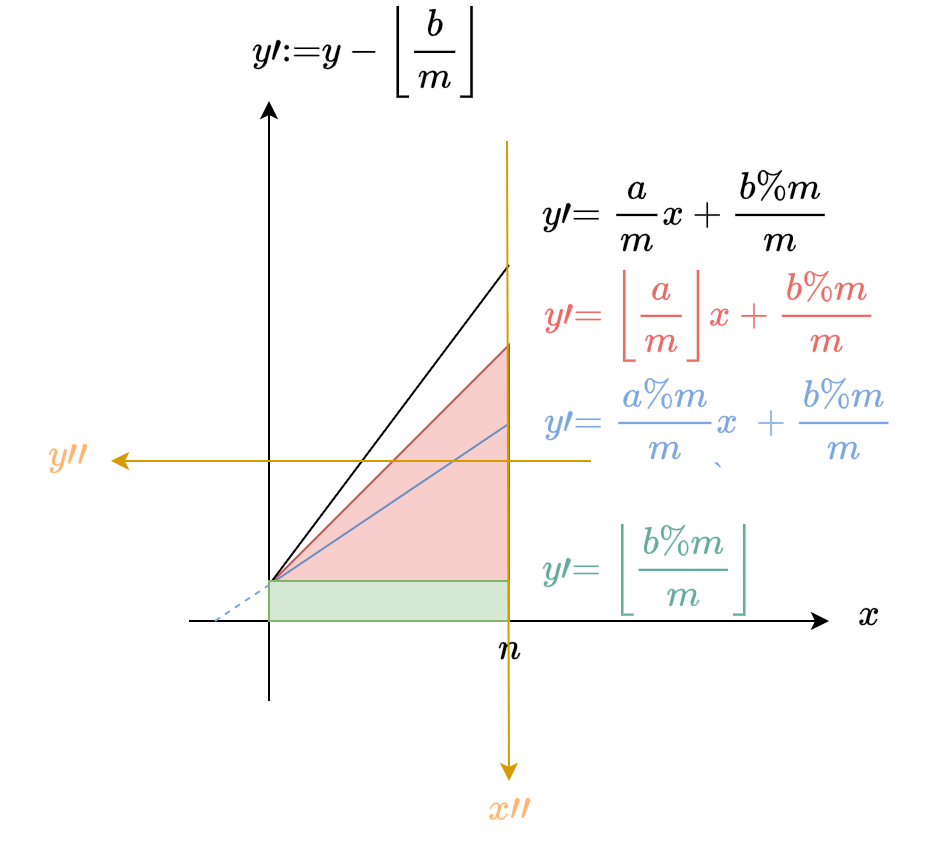
実はダルマ落としのように赤い三角形部分を切り落としてしまっても、 \(S_3\) からの格子点の数は変わりません。元の直線の傾きから赤い直線の傾きを引き、青い直線 \(y = \frac {a\%m} {m} + \frac {b \% m} {m} := y'(n)\) が現れます::

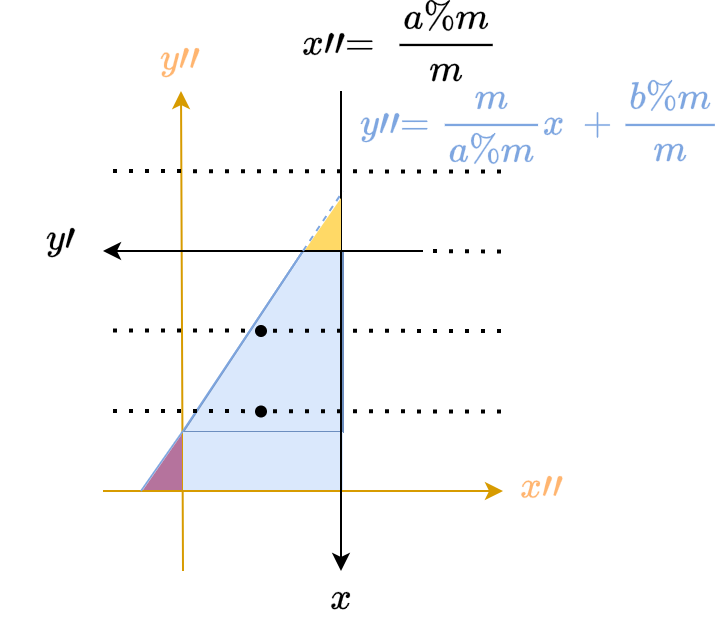
- 紫箇所は格子点の数に寄与しません。そもそも \(y''\) 軸が \(y' = y'(x)\) 中の最大の整数部分で切る線だからです。
- 黄色箇所は格子点の数に寄与しません。なぜなら青い直線の傾き \(\frac {a\%m} {m} < 1\) かつ y 切片 \(\frac {b\%m} m < 1\) のため、点線を伸ばしていくと \(x = -1\) に到達する前に \(y = 0\) になります。
ここで \(x, y'\) と \(x'', y''\) の関係を整理します。
これを肝心の直線 \(y' = \frac {a\%m} {m} x + \frac {b\%m} {m}\) に代入して整理します:
- \(y'(x) = \frac {(a\%m)x + b\%m} {m} := \frac {f(x)} {m}\) に対して \(m (y'(x) - \lfloor y'(x) \rfloor) = f(x)\%m\)
上図の \(x'', y''\) 座標系に注目します。紫部分を除去し黄色部分をくっつけることで、元の問題と同じ形に帰着できました。よって floor_sum は再帰的に計算できます:
計算式
\begin{equation} \mathcal{floorSum}(n, m, a, b) = \begin{cases} 0 \text{ if } m = 0, \\ 0 \text{ if } a = 0, \\ \mathcal{fromS_1} + \mathcal{fromS_2} + \mathcal{floorSum}(n, m, a\%m, b\%m) \text{ otherwise.} \end{cases} \end{equation}実装
再帰関数を書きました: Math/FloorSum.hs.
末尾再帰 & 正格評価の形 (返値を !acc 引数として引き回す形) に書き直しても、ジャッジ環境においては高速化されませんでした。 Haskellで再帰を心置きなく書いて良い理由 を見る限りでは !acc を書いて初めてサンクを潰せるように見えますが、実はコンパイラがよしなに正格評価してくれる気がします。関連: foldl vs. foldl'に終止符を打つ 。
計算量
傾きが大きいほど計算量が増え、 \(O(\log ma)\) らしいです。たぶん互助法の計算量と同じ? 今は理解する体力が残っていません……。
感想
消耗しました。この程度の数学に 1 週間を丸ごと費やすとは……絶望ですw
Floor sum (signed)
上記の floorSum において \(a \ge 0, b \ge 0\) の成約を取り外すことができます。応用的な問題で役立つらしく、これも読み込みたいです。