ARC 181
ARC 181 に参加しました。なんと D 問題が解けました! バイブスあげてこー!
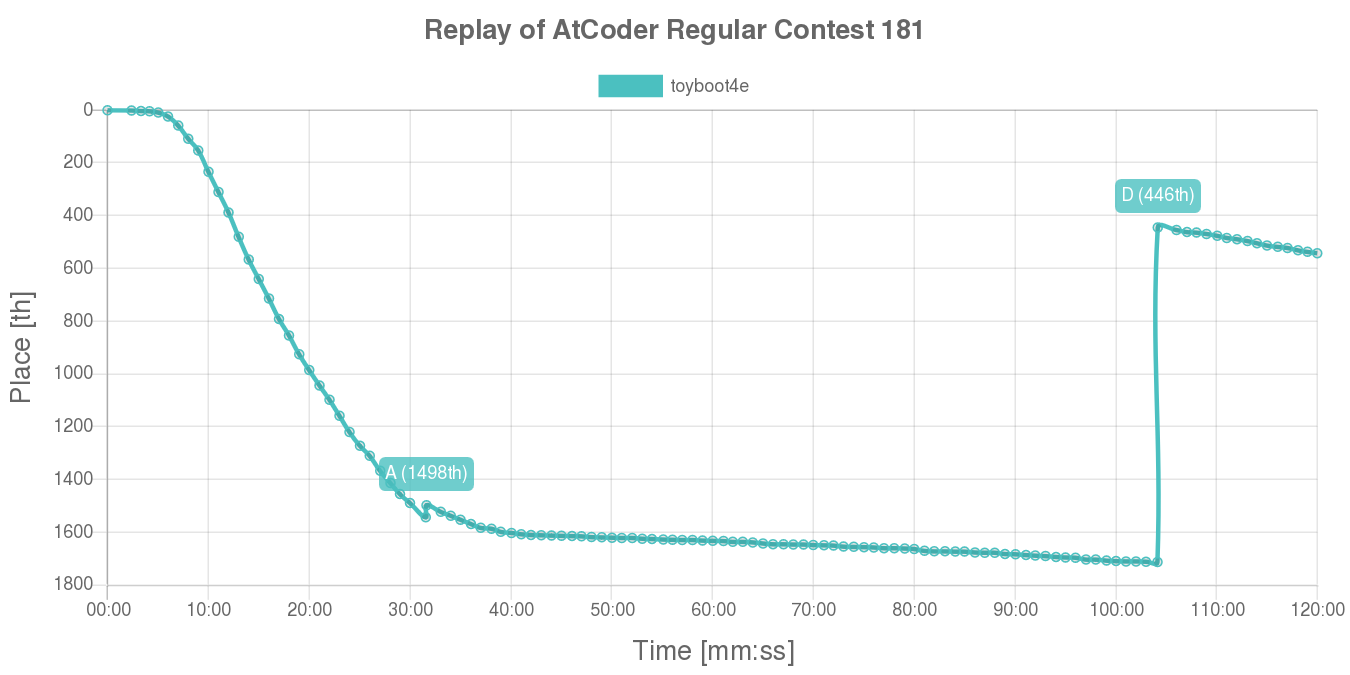
A 問題
35 分で解いて緑パフォ下位でした。
D 問題
JOI Bubble Sort 2 の解説 を見つけ、バブルソートでは 1 回の走査につき各点の転倒数がちょうど 1 下がることが分かりました。シミュレーションで解けました。
B, C 問題と比べても明らかに解説が薄く、本来 B 問題相当な気がします。それはそれとして、黄 diff の問題を本番で通せたのは最高でした。
ABC 366
ABC 366 に参加しました。 3 完!! バイブスが消え去りました。
| 問題 | A 問題 | B 問題 | C 問題 | D 問題 | E 問題 |
|---|---|---|---|---|---|
| 予想 | 5 | 400 | 300 | 1,300 | 1,200 |
| 実際 | 20 | 180 | 180 | 586 | 1,513 |
A 問題
Yes!
main=interact$f.map read.words;f[n,t,a]|((||)<$>(<t)<*>(<a))(n`div`2)="Yes"|0<1="No"
B 問題
下から上に読む不思議な問題でした。 transpose と dropWhileEnd を知っていると楽できますね。 dropWhileEnd は知りませんでした。
import Data.List;main=interact$unlines.map(dropWhileEnd(=='*')).transpose.map(++replicate 99'*').reverse.tail.lines
C 問題
std::multiset の verify 用の問題のようでした。自作の MultiSetを使いました。
クエリ処理の方法としては、 mapAccumL を使うか、 mapMaybeM で State モナドに Map を載せるのが正攻法だと思います。
D 問題
\(A_{x, y, z}\) を \(A_{z, y, x}\) だと思っていました (^ω^) (^ω^)
E 問題
マンハッタン距離は X, Y 成分毎に独立して考えられる性質が良いですね。 Upsolve するぞー
\(\sum_i |x_i - x_0|\) は \(x_0\) = 中央値 (xs をソートした時の真ん中の値) の時に最小です。中央値から [-D, +D] の範囲で \(x_0\) を動かしたときの \(\sum_i |x_i - x_0|\) の分布を \([0, D]\) の範囲で記録すれば解けると思います。 ー> 解けました。
2 分探索というのがピンと来ておらず、別解がありそうです。
Wavelet Matrix (1)
Wavelet Matrix の頭文字は WM. ウィンドウマネージャと同じくらい必須のデータ型かもしれません。つまり普通は使わないのでは……?
セグメント木が変域 (添字) の 2 分木とするならば、 Wavelet Matrix は値域の 2 分木と言えそうです。実際強力です。
概要
入力は座標圧縮済みの数列とします。上位 bit から順番に、その bit の 01 を基準に数列をソートしていきます。
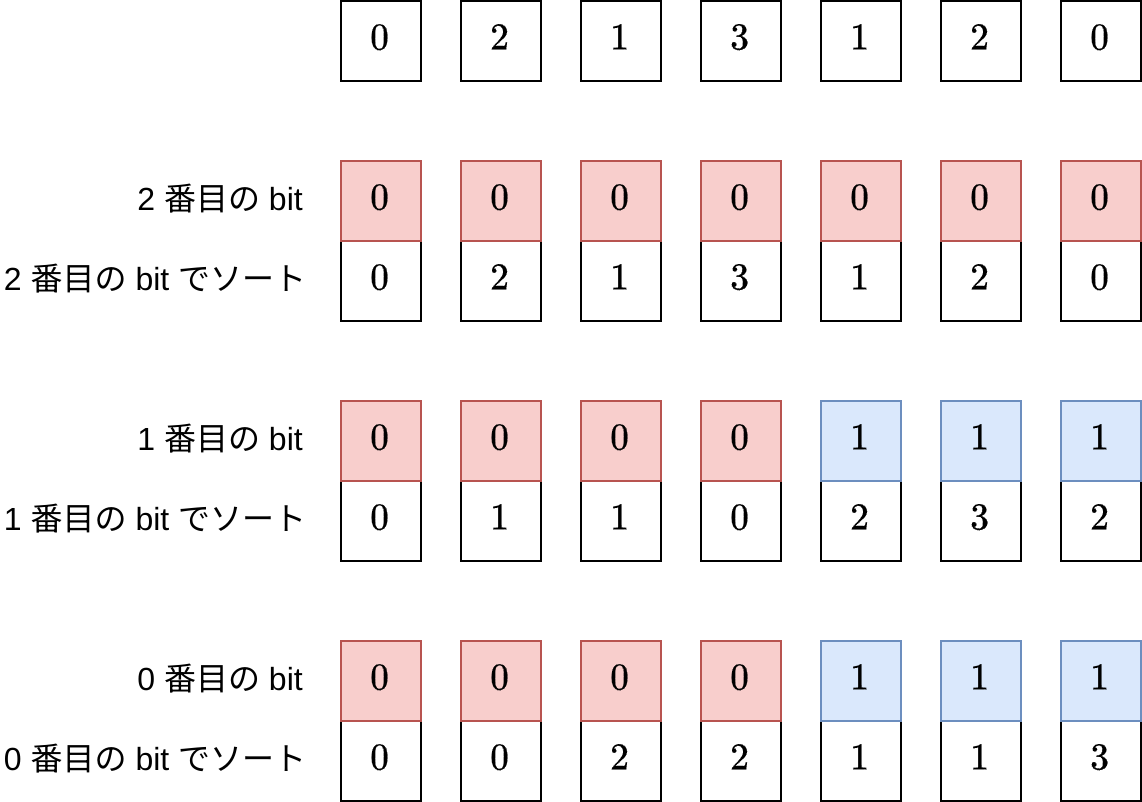
kthMin
各行の bit 列が wavelet matrix の本体です。たとえば \([l, r]\) 区間中の K 番目に小さい数を求めるためには、次のように上から下に降りていきます:
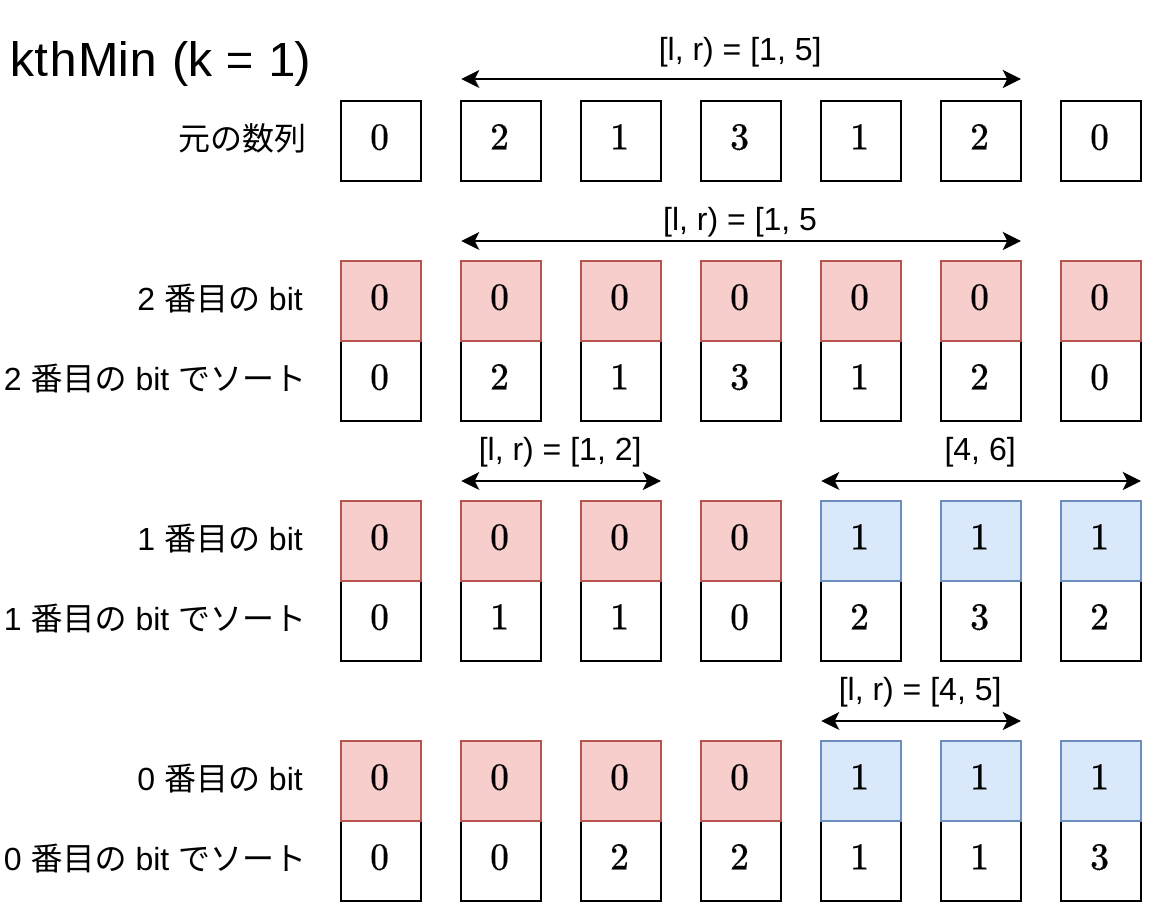
各行 (各 bit) で区間 <—> が 2 分されていきます。最下段まで降りるまでの bit 値は 0, 0, 1 の順番だったため、答えは 0b001 = 1 です。また区間が 2 分されるとき、左へ降りるか右へ降りるかを \(O(1)\) で判定するために、事前に各 bit の累積和を作成します。
freq
1 行降りる度に値域が 2 分されることから、区間内の \(|\{x | x \lt x_{ref}\}|\) も取得できます。
access
なお元の数列、ソート済みの数列は復元できるため削除します。また累積和では Word (64 bit) 単位で和を取ることで省メモリ化します。
情報源
以下 2 つから学びました:
- ウェーブレット行列(wavelet matrix) - Eating Your Own Cat Food
- NyaanNyaan/library/data-structure-2d/wavelet-matrix.hpp
気になる
- コンパクトデータ構造コンパクトデータ構造
ながたかなさんお気に入りの書です。 - naoya さんの Wavelet Tree (および参考文献)
これを読んで、まだまだインプットが足りないと自覚しました。
未読のコード
- NyaanNyaan/library/data-structure-2d/segment-tree-on-wavelet-matrix.hpp
- ei1333/library
- maspypy/library
Verify
[X]Range Kth Smallest[X]Static Range Frequency[ ]Rectangle Sum
Segment Tree on Wavelet Matrix?
未実装の API
Wavelet Matrix の機能はまだまだあるようです。
Misc
ポテンシャル付き Union-Find の抽象化
ポテンシャル付き Union-Find には非可換な群が載ります。
[X]Unionfind with Potential
126 ms. 重み付き Union-Find (可換群)[X]Unionfind with Potential (Non-Commutative Group)
319 ms. 重み付き Union-Find (非可換群)
参考: 重み付き Union-Find とそれが使える問題のまとめ、および、牛ゲーについて
遅延伝播セグメント木の型クラス
SemigroupAction とは別に SegmentTreeAction を作成しました。区間長を受け取る半群作用を使うと、モノイドに長さを載せなくて済んで便利です。
class SegmentTreeAction op a where
-- 半群作用 (セグメント木用)
{-# INLINE segAct #-}
segAct :: op -> a -> a
segAct op a = segActWithLength op a 1
-- 区間長を受け取る半群作用 (セグメント木用)
{-# INLINE segActWithLength #-}
segActWithLength :: op -> a -> Int -> a
segActWithLength op a _ segAct op a
Emacs
Ellama
話題の 最強ローカルLLM実行環境としてのEmacs に沿って Ellama を設定してみました。しかし手元の VRAM が小さく (8 GB), ローカル LLM を快適に動かすには至りませんでした。
著者の tomoya さんは Mac ユーザです。現代の Mac (M1 以降) はメモリが RAM 兼 VRAM として機能するらしく、 AI 時代には相性が良さそうですね。
org-ai
org-ai から gpt-4o を使い始めました。爆速ではないか……!
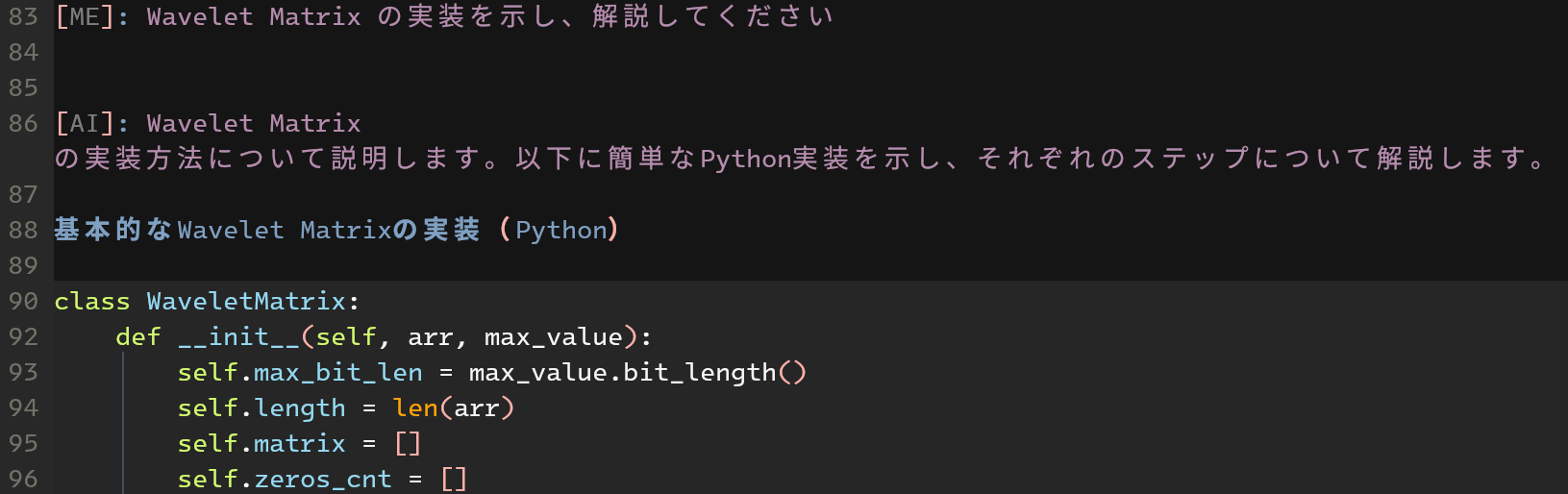
やはりブラウザよりも使い勝手が良いです。フロントエンド (コマンド) も充実していて応用が効きそうです。
Deno くん?
いいですねー。
— Deno (@deno_land) August 9, 2024
関係無いですが、 Gopher くんキーキャップが欲しいです。
Gopherキーキャップとても良い pic.twitter.com/h2JuN42zY2
— uji (@uji_rb) March 8, 2022
HS 5
スタジオモニターの YAMAHA HS 5 を買いました。スピーカーなのにちゃんと鳴って良かったです。耳と高さが合わないと良さが 3 割減なので、 FlexiSpot を買わねばと思います。