ARC 182

ARC 182 に参加しました。

A 問題

各操作で点 \(P_i\) を基点に右または左へ chmax 操作をします。過去と未来の \((P_i, V_i)\) を元に各操作が可能な方向に制約が課せられると考えて、矛盾しない場合は \(2^{\mathcal{nFree}}\) が答えです。

B 問題

こちらの方が解かれている……？？

ABC 367

ABC 367 に参加しました。 C 問題で崩壊しましたが、灰 diff でしたか……

Table 1: Diff 予想
問題 A 問題 B 問題 C 問題 D 問題 E 問題 F 問題
予想 200 300 1,100 1,200 1,000 1,800
実際 43 43 234 1,037 1,370 1,540

A 問題

起床時刻を基点として 定刻 < 起床時刻 \(\pmod {24}\) ならば "Yes"!

main=interact$f.map read.words;f[a,b,c]|mod(b-c)24>mod(a-c)24="Yes"|0<1="No"

B 問題

末尾の 0 と . を切り落とします:

import Data.List;main=getLine>>=putStrLn.dropWhileEnd(=='.').dropWhileEnd(=='0')

C 問題

七転八倒して 6 進数を列挙して解きました。リストを使うべきですね。

let result :: [[Int]]
    result = inner 0 $ U.toList constraints
      where
        inner !acc []
          | acc `mod` k == 0 = [[]]
          -- 一応枝刈りしました:
          | otherwise = []
        inner !acc (a : as) = do
          d <- [1 .. a]
          -- map == (<$>)
          -- 再帰的なリスト内包表記が書けないマンです
          (d :) <$> inner (acc + d) as

ちなみに bytestring の Builder 生成は foldMap' よりも foldMap の方が速かったです。いずれも print まで遅延される気がしていましたが……。

D 問題

円環上の頂点を幅 (N - 1) の窓で見ます:

1---2---3---4---1---2---3---4
x---o---o---o
.   x---o---o---o
.   .   x---o---o---o
.   .   .   x---o---o---o

整理後、以下の形になりました:

solve :: StateT BS.ByteString IO ()
solve = do
  (!n, !m) <- ints2'
  !ds <- intsU'

  let !sumMod = U.sum ds `mod` m

  -- 各点の位相 (各点の位置 mod m):
  let !pos = U.init $ U.scanl' (addMod m) (0 :: Int) ds

  -- 位相の分布 (distribution):
  !dist <- U.unsafeThaw $ U.accumulate (+) (U.replicate m (0 :: Int)) $ U.map (,1) pos

  -- カウンタを `StateT` に載せて以下の処理を実施する:
  printBSB <=< (`execStateT` (0 :: Int)) $ U.forM_ pos $ \x -> do
    -- x を分布から消す:
    -- x---o---o---o
    GM.modify dist pred x
    -- x と同相の点数をカウントに追加する:
    modify' . (+) =<< GM.read dist x
    -- 尺取り虫:
    -- .   o---o---o---o
    GM.modify dist succ (addMod m x sumMod)

E 問題

ダブリングの API を再整理しました。

solve :: StateT BS.ByteString IO ()
solve = do
  (!n, !k) <- ints2'
  !perm <- U.map pred <$> intsU'
  !xs <- intsU'
  printVec $ sactTimes k (Permutation perm) xs

One-shot なダブリングは stimes (の正格評価版) で実施すべきですね。半群作用の形にすればなおヨシ！

F 問題

一瞬 Mo を考え、すぐに解けないことが分かりました。もうっ

Wavelet Matrix (2)

追加の API

ran (freq, count)

後述します。

lookupGT wm x

kthMin wm (countLE wm x) の形で実装できます。

Segment Tree on Wavelet Matrix

先週の図を前提として、 rank (freq, count) や fold は以下のように実装します:

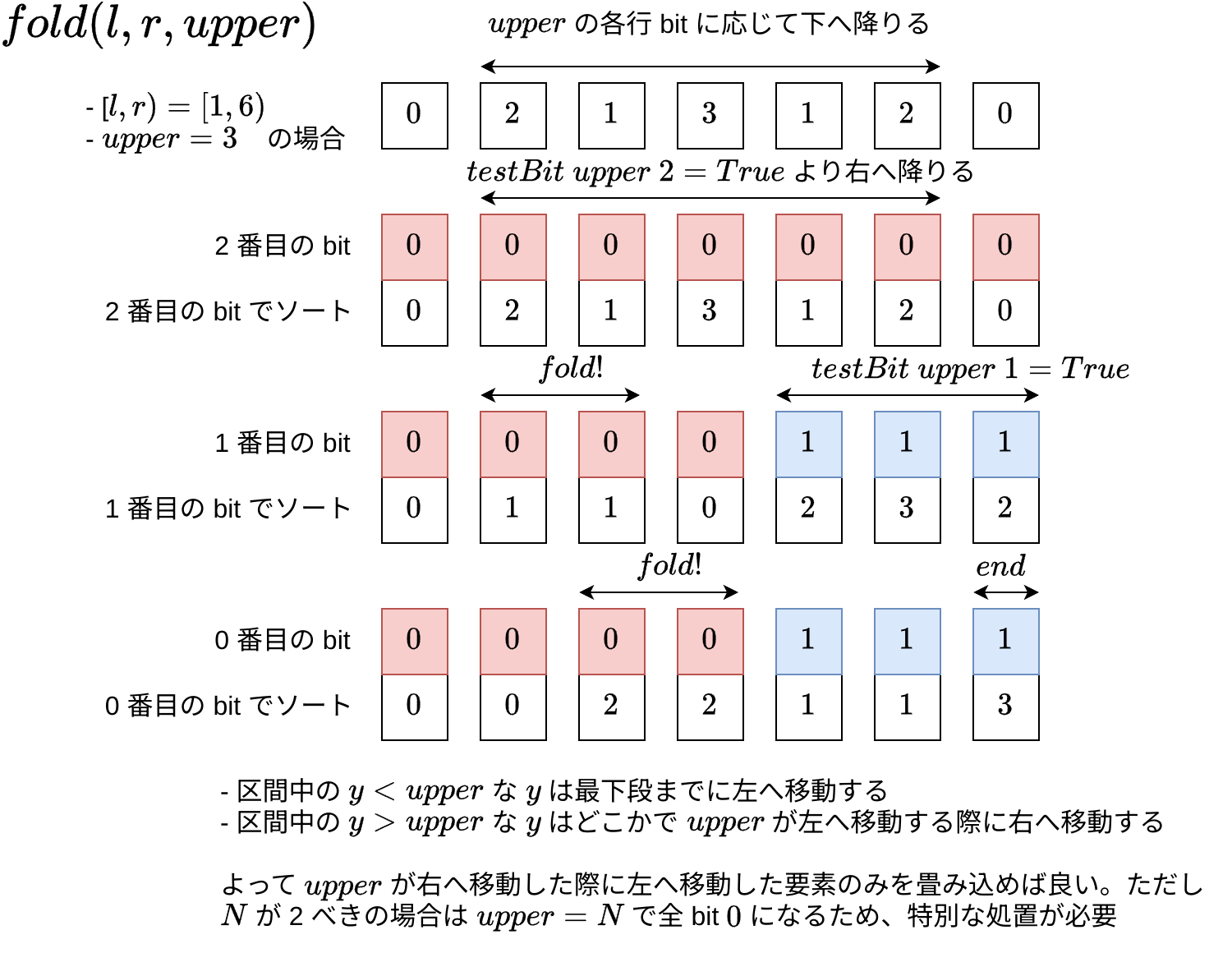
2024-08-18-segment-tree-on-wavelet-matrix-1.png

たとえば 2 番目の 1 に注目すると、ちょうど 1 回だけ fold の対象になっていることが分かります:

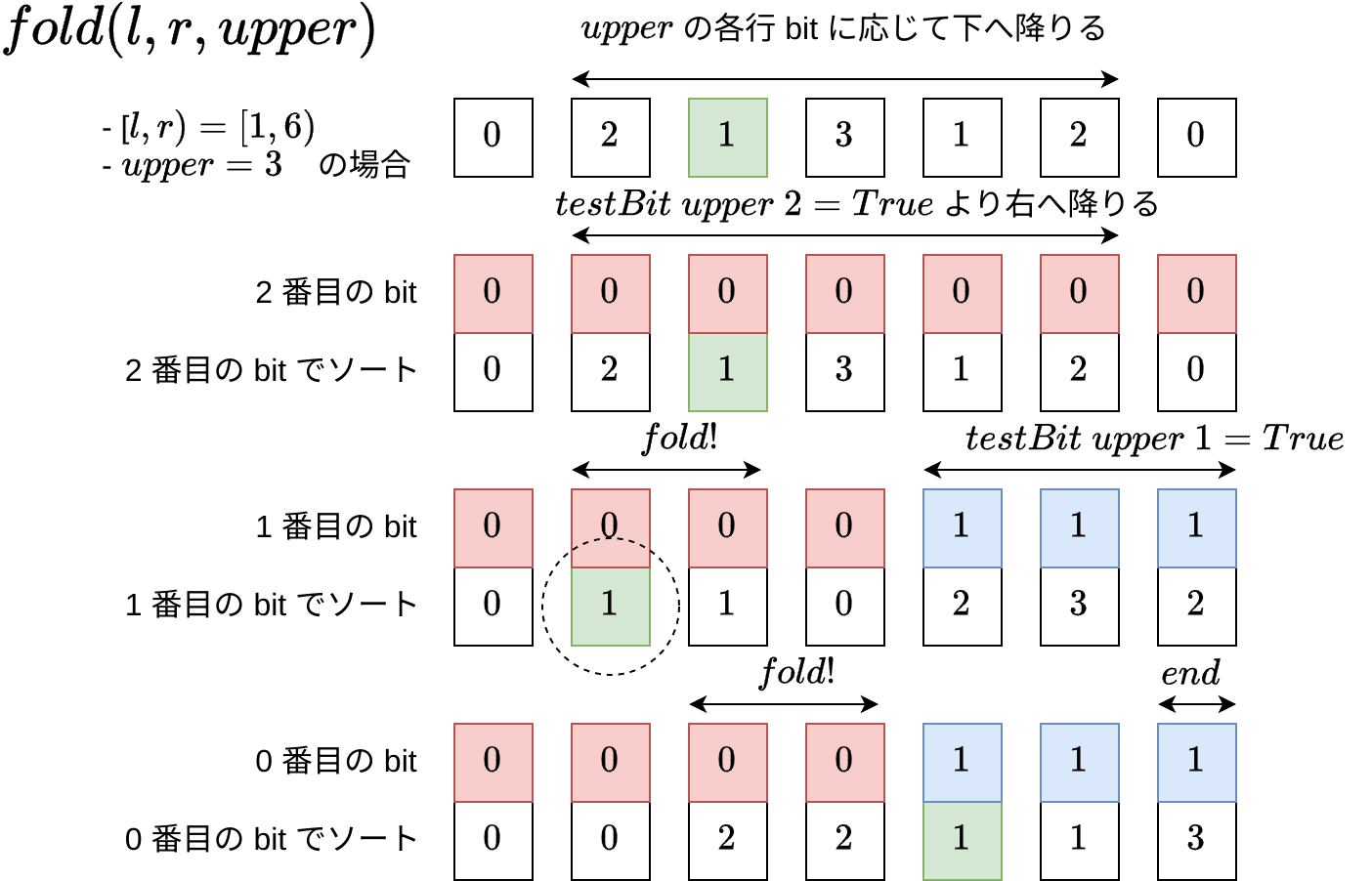
2024-08-18-segment-tree-on-wavelet-matrix-2.png

したがって bit 毎に (各行に) セグメント木を持って畳み込めば、 freq と同じ要領で fold を実装できます。凄いなー……

Distinct count

[l, r) 区間中の重複しない要素数を数えよ。これも Wavelet Matrix で解けるようです。

-- 重複する点を数える。以下のように近隣の重複点の位置を WM に入れる:
--
-- input      A  .  .  A  .  A  .  A
-- i          0  1  2  3  4  5  6  7
-- input'     -        0     3     5
--                     <----->        [3, 5] 中の x \in [3, 5] の数は 1 (重複数が 1)
--                     <----------->  [3, 7] 中の x \in [3, 7] の数は 2 (重複数が 2)

Distinct kthMin

思いつきません。

実際、 Wavelet Matrix に使い道はあるのか

機能豊富かと思いきや、高速なのは特殊な操作ばかりでした。役立つかはかなり疑問です。

Misc

最近買った本

買っただけです。

セール