ABC 371
ABC 371 に参加しました。 B → A → D → E → C の順に解くことになった危険な回でした。
FIXME: 間違っている
| 問題 | A 問題 | B 問題 | C 問題 | D 問題 | E 問題 |
|---|---|---|---|---|---|
| 提出 | AC | AC | AC | AC | AC |
| Diff 予想 | 5 | 300 | 600 | 800 | 1,700 |
| Diff 結果 | 11 | 84 | 228 | 1,088 | 1,453 |
A 問題
A, B, C の大小関係が与えられたとき、真ん中の要素がどれか答えよ。 6 パターンを網羅しました。
solve :: StateT BS.ByteString IO ()
solve = do
ss <- words . BS.unpack <$> line'
printBSB . ("ABC" !!) $ case ss of
-- a -> b -> c
["<", _, "<"] -> 1
-- a -> c -> b
[_, "<", ">"] -> 2
-- b -> c -> a
[_, ">", "<"] -> 2
-- b -> a -> c
[">", "<", _] -> 0
-- c -> a -> b
["<", ">", _] -> 0
-- c -> b -> a
[">", _, ">"] -> 1
Prolog を試しましたが、入力処理が無限ループして EoF エラーになりました。まったく糸口の掴めない言語です。
B 問題
それぞれの村で最初に生まれた男児を判定せよ。村ごとに最初に生まれた男児を記録してから、答えを計算します。
solve :: StateT BS.ByteString IO ()
solve = do
(!n, !m) <- ints2'
abs <- U.replicateM m ((,) <$> int' <*> char')
let !initials = U.update (U.replicate n (maxBound @Int))
. U.reverse
$ U.imapMaybe (\i (!a, !b) -> if b == 'M' then Just (a - 1, i) else Nothing) abs
let !res = U.imap (\i (!a, !_) -> initials G.! (a - 1) == i) abs
U.forM_ res printYn
C 問題
グラフ G をグラフ H と『同型』にするための最小コストを求めよ。 G, H の頂点の対応 (順列) を全探索して答えます。
D 問題
座標圧縮して累積和を取得する典型問題です。累積和を半開区間で取得することにすると、実装が楽です。しかし僕は常に閉区間を使っています。したがって下の図のように ← 方向の 2 分探索も必要で詰まりました。
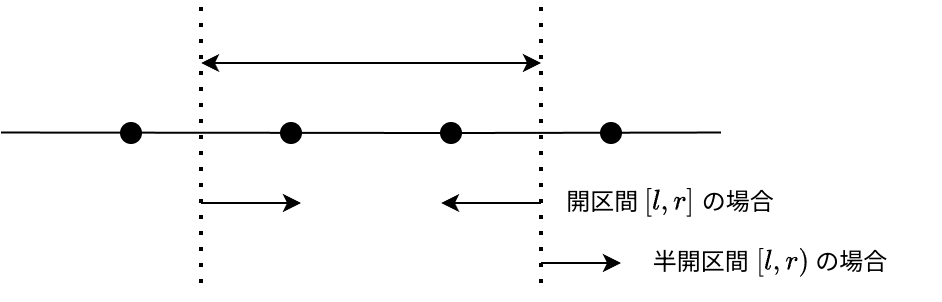
今のところ閉区間で得した経験は皆無です。めぐる式 (?) を採用したので、右から左へ伸ばす 2 分探索も やや 直感的になりました。
let solve l r
| l' == -1 || r' == -1 = 0
| otherwise = csum +! (l', r')
where
!_ = dbg ((l, r), (l', r'))
l' = fromMaybe (-1) $ bisectR 0 (G.length dict - 1) $ \i -> dict G.! i < l
r' = fromMaybe (-1) $ bisectR (G.length dict - 1) 0 $ \i -> r < dict G.! i
let !res = U.map (\(!l, !r) -> solve l r) qs
putBSB $ unlinesBSB res
E 問題
数列 \(\{A_i\}_i\) に対して各 \([l, r] (l \le r)\) 区間中の要素数の和を求めよ。愚直に計算すると \([l, r]\) 区間の取り方が \(\frac {N (N + 1)} {2}\) 通りであり、区間ごとの要素数のカウントにも \(N\) 回程度の計算が必要です。高速化を目指します。
区間の大きさを広げていくとき、集合の要素数は単調増加します。また要素数への寄与は、集合の要素毎に独立して計算できます。値ごとに集合に含まれない場合の数を高速 (合計 \(N\) 回程度) で計算できることが分かり、全事象から余事象を引いて \(O(N)\) で解けます。
実装は cojna さんの zipWith を使った提出 が良かったです。けっこう難しい問題だと思いましたが、主客転倒の問題としては基礎的な方だったかもしれません。
AHC 037 (短期コン)
AHC 037 に参加しました。頂点を追加して最小コストの全域木を作れ。ただし辺で繋がれた 2 頂点の関係は \(x_1 < x_2\) かつ \(y_1 < y_2\) に限る。といった問題でした。
頂点を y, x の順でソートすると、ナップサック問題の要領で最小コストを計算できます。後はランダムに頂点を追加し、スコアが上昇する場合は採用としました。

ランダムな方法では 9 割方スコアが減少するようで、僅かな頂点しか追加できませんでした。貪欲解に頂点を追加する方法があるようなので、解説放送見るなどして upsolve したいです。
gksato さんの提出が相当なハイスコアでした。理解したいです。
#AtCoder #AHC037 with Haskell
— 符号/gksato (@Fine_sugar_hill) September 15, 2024
score 5,388,249,433 (rank 23)
焼きなましとか何もわからなかったので、「binary tree(正確には、入力に含まれず(0,0)でもない飲み物の頂点は次数が3である)として良い」ことを使ってただ葉から貪欲をして、それをただ1回提出しました。結果に驚いています。
Misc
競プロ
- PAST (リアルタイム受験)
見送りました。 - Libary Checker
そろそろ再開したいと思います。憧れの link/cut tree がまったく理解できないので、写経から始めます。
ブログ
AsciDoc で言うところの callouts を org-mode 上で再現しました。
{
inputs = { # 1
nixpkgs.url = "github:NixOS/nixpkgs/nixpkgs-unstable";
nixpkgs-stable.url = "github:nixos/nixpkgs/nixos-24.05";
};
outputs = { self, nixpkgs, home-manager, org-babel, emacs-overlay, ... }: {
nixosConfigurations = (import ./hosts/tbm { # 2
inherit self nixpkgs home-manager;
});
};
}
fcitx5-mozc メモ (NixOS)
mozc_toolの場所
/run/current-system/sw/binから消えていました。本来は.desktopファイルが作られるべきですから、コントリビュートチャンスでしょうか。home-managerも確認が必要です。
$ nix eval nixpkgs#fcitx5-mozc.outPath "/nix/store/7iwjmjfvbwc1q8qgfh9ban5xzq5rjmjj-fcitx5-mozc-2.26.4220.102" $ /nix/store/7iwjmjfvbwc1q8qgfh9ban5xzq5rjmjj-fcitx5-mozc-2.26.4220.102/lib/mozc/mozc_tool --mode=config_dialog- IME の ON/OFF で日本語・英語を切り替える
キーバインドからToggle Alpha なんとかを消しました。