ABC 376

ABC 376 に参加しました。

Table 1: Diff 予想
問題	A 問題	B 問題	C 問題	D 問題	E 問題	F 問題
提出	4:48	11:52	19:46	28:09	49:35	96:17
予想 diff	100	400	400	1,000	1,200	1,600
実際 diff	19	290	366	743	1,063	2,089

226 位を取ってレーティング爆上がりです。

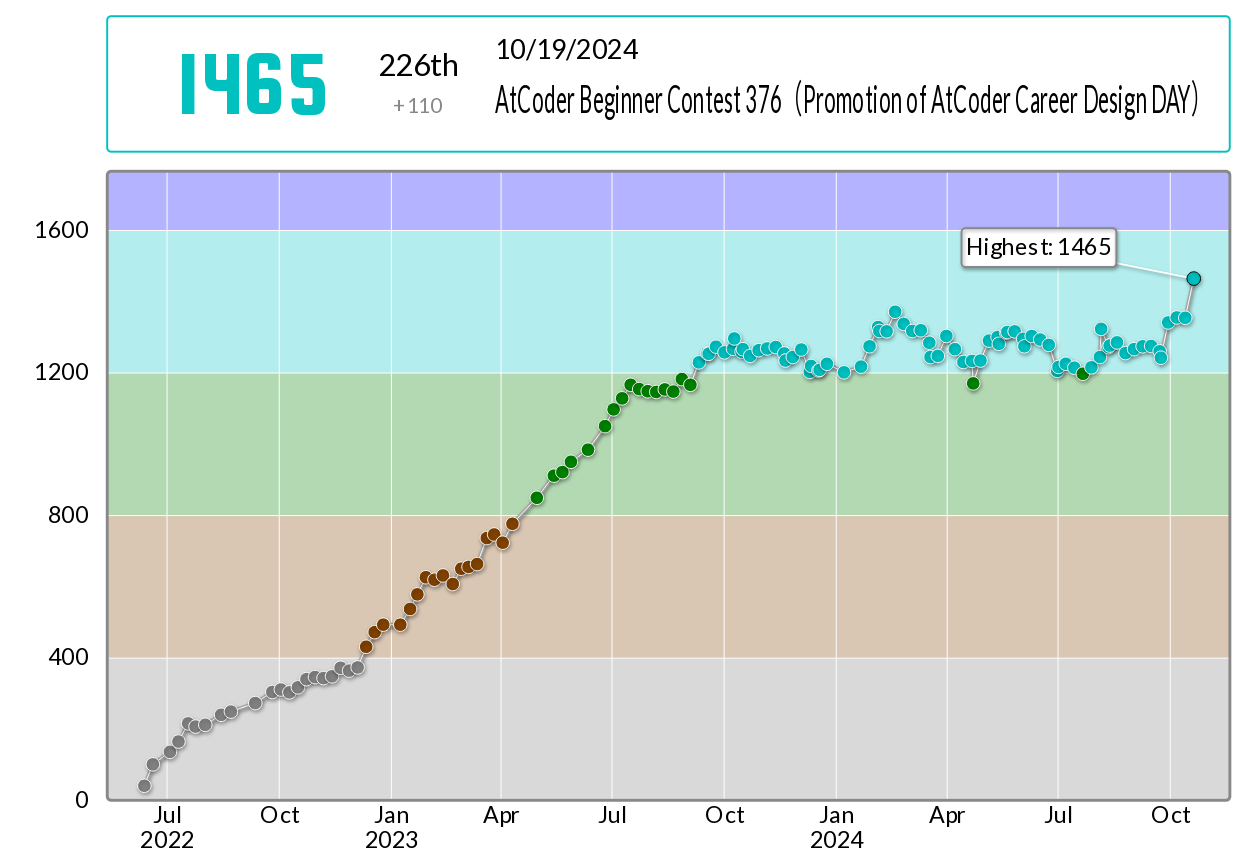
レーティングは適正値へ収束していくものなので、今後の大敗は覚悟します。悔しいだろうなー……

A 問題

単調増加数列の隣接項の差が $c$ 以上となるように項を間引く時、残った数列の最大の長さを求めよ。最終項を状態として畳み込みます。

main=interact$show.f.map read.tail.words;f(c:a:t:r)|t-a<c=f(c:a:r)|0<1=1+f(c:t:r);f _=1

B 問題

円環上の 2 物体に対し (物体, 移動先) の形で操作指令が与えられる。物体同士が衝突しない方向に指定の物体を動かして、操作指令を実行せよ。

円環を開きます。正方向の回転の可否を $L < R'$ かつ $L < T'$ となる最小の $R', T'$ ($R' \equiv R \bmod N, T' \equiv T \bmod N$) を使って検証します。移動経路中に $R'$ があるかを inRange で判定すれば良いです。

負方向の回転も、同様に $R' < L$ かつ $T' < L$ となる最大の $R', T'$ を使って検証します。

C 問題

$N$ 個の物体と $N - 1$ 個の箱がある。 大きさ(物体) <= 大きさ(箱) となるようマッチングさせたとき、余る物体を可能な限り小さくせよ。

物体、箱をそれぞれ降順ソートし貪欲にマッチングすれば $O(N \log N)$ で解けます。未証明ですが。

-- 降順ソートされた [物体], [箱] を引数に ([余った物体],[余った箱]) を返す
eat :: [Int] -> [Int] -> ([Int], [Int])
eat = inner ([], [])
  where
    -- 物体が無くなった場合
    inner (!ls, !rs) [] restR = (ls, rs ++ restR)
    -- 箱が無くなった場合
    inner (!ls, !rs) restL [] = (ls ++ restL, rs)
    -- 箱も物体もある場合
    inner (!ls, !rs) (x : xs) (y : ys)
      -- 物体と箱がマッチする (物体 <= 箱)
      | x <= y = inner (ls, rs) xs ys
      -- 物体 x を余った物体の列に移動する
      | otherwise = inner (x : ls, rs) xs (y : ys)

D 問題

辺に重みを持つ有向グラフが与えられる。始点を頂点 1 として、最小閉路の長さを求めよ。

これが茶 diff なのはヤバい……。知っていたことは以下です:

強連結成分分解 (SCC) は functional graph でのみ有効です
- 有向グラフでは、多分すべての閉路が釣れてしまい、絞り込みが必要です
  - 頂点 1 を含む SCC に対する DP で解ける気はします
- なお無向グラフでは無意味です
閉路検出の問題では 1 つの閉路を復元しますが、最短の閉路は取れません。

DFS で全経路を見ると、明らかに TLE します (極端に言えば密グラフでは $O(N!)$ です) 。

多重始点の Dijkstra 法に帰着しました。すなわち頂点 1 から出た重み付き辺の集合 $\{(v_i, w_i)\}_i$ を距離一覧やヒープの初期値とし、 Dijkstra 法を実施します。面白い！

公式解説では、到達までの辺の数が $K$ となる頂点の集合を求めていました。これは難しい。

原案は evima さんでした。流石です。

ABC376おつかれさまでした。Dの原案でした。（一周回ってまだ出ていなかったはず……）（解説動画の代わり？に https://t.co/l1nO3LswU9 があります。）
— えびま (@evima0) October 19, 2024

E 問題

数列 $\{(A_i, B_i)\}_i$ から $K$ 項を選ぶとき $\mathrm{max} \{A_i\}_i \cdot \sum_i B_i$ を最小にせよ。

$\mathrm{max} \{A_i\}_i$ を全探索すると効率的に解答できます。すなわち $\{(A_i, B_i)\}$ を昇順ソートし、最初の $K$ 項を初期値に畳み込みます。状態としては $\sum_i B_i$ と multiset を持てば良いです。

けっこう難しい。

F 問題

B 問題の設定において、未指定の物体も動かしても良いとする。対象の物体は正方向と負方向のどちらに回せることになり、状態数が跳ね上がります ($2^Q$) 。

その状態数を一定数のスロットに削減するのが DP! 2 物体の位置 $(l, r)$ をキーに Map で緩和すると $O(NM \log N)$ ぐらいで解けました (運！) 。対象の物体は必ず同じ位置で止まりますから、 $|\{(l_i, r_i)\}_i| = O(N)$ なんですね。

感想

Library Checker で閉路検出を経験したため、 D 問題をスムーズに考察できました。 Library Checker は良いぞー

Haskell

次の言語アップデート

ac-library-hs を作りますを投稿しました。リポスト・ライク等ありがとうございました！

関心のトピックは Issue に上げており、開発が進めばまたブログにします。アドベントカレンダーにも投稿するかも。

案: プロジェクトを提出する

ジャッジに細工すれば、プロジェクトを丸ごと提出できるようにできます。確実に qualified import ができてアリかも。

Listing 1: 提出ファイル (イメージ)

{- AC_PROJECT src/MyLib/F.hs -}
module F (f) where

f :: Int -> Int
f = (+ 1)

{- AC_PROJECT app/Main.hs -}
import MyLib.F qualified as F

main :: IO ()
main = print $ F.f 1

Listing 2: 展開結果 (イメージ)

.
├── app/
│  └── Main.hs
└── src/
    └── MyLib/
        └── F.hs

`ac-library-hs` で注目のパッケージ

recovery-rtti
Show a 制約が無くとも anythingToString できるスグレモノです。 Haskell の森に紹介があります。デバッグに役立つ他、詳細なエラー出力に使用すべきか検討中です。
tasty-rerun
tasty で失敗したテストのみを再実行する機能です。助かる！
```
  $ cargo test --test-options --rerun
```
tasty-golden, tasty-silver, hspec-golden
insta みたいにエラー出力をテストするために使いたいです。

本物のプログラマはHaskellを使う

本物のプログラマはHaskellを使う。一連の記事が響くようになって来ました。 QuickCheck の記事などを読んでいます。

`FastMutInt`

StateT vs IORef: a benchmark - r/haskell にて FastMutInt を知りました。

結局中身は ByteArray# なので、 MutablePrimArray と速度は変わらない気がします
PrimMonad ではなく IO が要求されます

Misc

Emacs 秋フェス

調子に乗って Emacs 秋フェスの登壇枠を取っていました。 leaf, Evil 辺りの当たり障り無い話をしようと思っています。 Embark, activities,bufler, popper など最近のパッケージを調べてみても良いかも。

Pixiv は怖過ぎるものの、エディタバーが楽しみ過ぎる！

我は陰の者、前日の Nix Meetup には参加できません。 Emacs 勉強会自体、ハードル高杉建築でした。